Задача 1.
Расставьте натуральные числа от 1 до 8 в кружки фигуры так, чтобы сумма чисел расположенных на каждой из пяти окружностей была одной и той же, и докажите, что такая расстановка единственная.
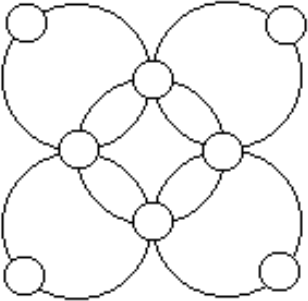
Задача 2.
Четыре гномика поселились в клетках квадрата 2 × 2. Утром гномики, живущие в соседних по сторонам клетках, пожали друг другу руки. На следующий день они поселились в домики по-другому и опять пожали руки соседям. На третий день всё повторилось. Могло ли оказаться так, что каждый пожал каждому руку ровно 2 раза?
Задача 3.
Из шахматной доски вырезали 2 квадратика 2 × 2. Докажите, что оставшуюся часть доски всегда можно разбить на доминошки. (Доминошка — фигура, состоящая из двух соседних по стороне клеток.)
Задача 4.
Настя записала в тетрадь число 29 102 018. Она хочет, переставляя местами две цифры, получить как можно большее число. Какое минимальное число перестановок ей придётся сделать?
Задача 5.
Серёже приснилось натуральное число и он начал прибавлять к числу его предпоследнюю цифру. После 99 таких операций он проснулся и смог вспомнить только число 56 789. Могло ли такое быть?

