Задача 1.
Какое наибольшее количество шестиклеточных сапожков можно вырезать из клетчатого квадрата 7 × 7?

Задача 2.
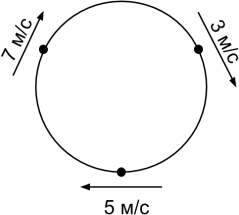
Три бегуна находятся на круговом стадионе длиной 300 метров, при этом каждый бегун находится на одинаковом расстоянии от двух других бегунов. Они начинают бежать по часовой стрелке со скоростями 3 м/с, 5 м/с и 7 м/с соответственно, при этом бегуны расположены так, как на рисунке. Через какое время они впервые окажутся в одной точке стадиона?
Задача 3.
Известно, что в семье не более 40 детей. Каждому из детей в семье задали вопрос: «Во сколько раз у тебя больше братьев, чем сестёр?» Были получены несколько ответов «в 7 раз» и несколько ответов «в 5 раз», при этом все дети сказали правду. Какое количество мальчиков может быть в этой семье?
Задача 4.
Доску 11 × 11 заполняют числами от 1 до 121 по следующему правилу: в первой строке слева направо записаны числа от 1 до 11 в порядке возрастания, во второй — слева направо от 12 до 22 в том же порядке, и так далее. Может ли сумма в клетках, образующих Z-тетрамино, быть равной 222? (Z-тетрамино можно как угодно поворачивать и переворачивать.)
Задача 5.
Вокруг большой лужи встали 20 жителей острова рыцарей и лжецов (рыцари всегда говорят правду, лжецы всегда лгут) и посмотрели на неё. Потом каждый из 20 людей грустно сказал: «Среди следующих трёх людей справа от меня по кругу есть хотя бы 2 рыцаря». Сколько среди них было рыцарей?
Задача 6.
В наличии имеется мягкая верёвка длиной 1 метр и деревянная палочка длиной 7 см. Докажите, что с помощью этих инструментов можно отмерить любую длину от 11 до 17 см, выраженную целым числом сантиметров.
Задача 7.
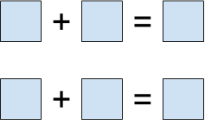
Есть 2 примера на сложение двух чисел. В каждый квадратик разрешается вписать любое натуральное число. Когда все 6 чисел вписаны (в обоих примерах вписаны оба слагаемых и сумма), игроки выясняют, сколько примеров на доске являются верными. Если хотя бы один пример верен, то выигрывает второй игрок, иначе выигрывает первый игрок. Кто выиграет и как ему нужно играть?
Задача 8.
Какие цифры могут быть заменены буквой Ь во всех решениях ребуса: АЛЬФА + АЛЕФ = ФИЛИН. (Одинаковыми буквами заменены одинаковые цифры, разными — разные.)

