Задача 1.
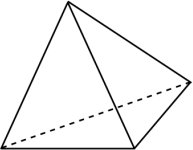
В каждую из четырёх вершин тетраэдра (см. рисунок). Никита написал натуральное число. Потом пришла Катя и посчитала для каждой грани этого тетраэдра сумму трёх чисел в вершинах этой грани. Могли ли у Кати получиться числа 2017, 2019, 2021 и 2023?
Задача 2.
Том может покрасить один забор за 8 часов, а Гек за 12 часов. Том и Гек решили вместе покрасить 5 заборов. От осознания объёма работы, которую они в итоге выполнили за 5 суток непрерывной работы, их работоспособность упала в несколько раз. Во сколько раз упала их работоспособность?
Задача 3.
Можно ли в каждую клетку квадрата 4 × 4 записать одну из цифр 1, 2, 3 или 4 так, чтобы в клетках любой фигуры T-тетрамино, расположенной внутри этого квадрата, не было одинаковых цифр?
Задача 4.
Однажды на турнире завтрак проходил в необычном формате. На очень большом столе по кругу было расставлено 200 тарелок, в каждой тарелке была каша одного из 20 видов, при этом тарелок с кашей каждого вида было ровно по 10 штук. Докажите, что можно выбрать 90 подряд идущих в кругу тарелок так, чтобы выбранные тарелки содержали каши хотя бы 10 различных видов.
Задача 5.
Вася посетил математический турнир и рассказал, что там было 2018 участников (Вася — один из 2018), и каждому из них среди остальных участников были знакомы ровно один мальчик и ровно одна девочка. Докажите, что Вася что-то напутал.
Задача 6.
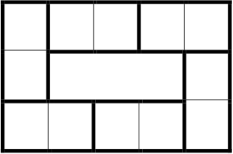
Лёлик разделил шоколадку 6 × 6 на несколько частей. Болик заметил, что если теперь провести любую прямую линию длины 6 по линиям сетки от края до края шоколадки, то она разделит на 2 части хотя бы три фигуры из разбиения Лёлика. Покажите хотя бы одно возможное разбиение Лёлика.
Задача 7.
Из комплекта домино потеряли все дубли, после чего из оставшихся костей выбрали 6 и составили замкнутую цепь, в которой кости лежали по правилам домино (см. рисунок). Найдите наименьшее возможное суммарное количество точек на всех доминошках цепи.
Задача 8.
У нумизмата есть 8 одинаковых на вид монет, которые весят соответственно 30, 31, 32, 33, 34, 35, 36, 37 граммов. Также в наличии имеются испорченные двухчашечные весы, которые показывают верный результат взвешивания только в том случае, если разница весов на чашках превышает 4 грамма, если же разница весов меньше либо равна 4 граммов, то весы остаются в равновесии. Как с помощью этих весов определить вес каждой из монет?

