Задача 1.
В пяти кучках лежит соответственно 1, 1, 1, 1 и 4321 камень. Разрешается выбрать любые четыре кучки из этих пяти, разбить эти четыре кучки на две пары, и в каждой паре переложить 1 камень из одной кучки в другую. Можно ли такими операциями сделать так, чтобы во всех кучках было поровну камней?
Задача 2.
Крош и Ёжик по очереди (начинает Крош) ставят в клетки таблицы 5 × 5 натуральные числа от 1 до 25 (каждое число можно использовать только один раз, в клетку можно ставить только одно число). Если после заполнения таблицы найдётся строка или столбец с суммой чисел 70, выигрывает Крош, в противном случае — Ёжик. Кто выиграет при правильной игре?
Задача 3.
Найдите наибольшее натуральное число, в десятичной записи которого нет нулей и одинаковых цифр, при этом для любых двух цифр этого числа верно, что одна из цифр нацело делится на вторую.
Задача 4.
Очередную олимпиаду решили провести по странным правилам: от 99 городов на олимпиаду отправляют по 2 участника – мальчика и девочку. После этого все 198 участников пытаются сесть за один круглый стол так, чтобы между любыми двумя детьми из одного города в круге сидели ровно 3 других участника. Докажите, что рассадить таким образом участников не получится.
Задача 5.
В ряд лежит 10 монет, среди них 8 настоящих и 2 фальшивые, причём фальшивые монеты лежат рядом и весят одинаково (настоящие монеты тоже весят одинаково). Фальшивые монеты весят легче настоящих. Как за 2 взвешивания на чашечных весах без гирь найти обе фальшивые монеты?
Задача 6.
Из Солнечного города в Изумрудный вышел Василий Иванович. Одновременно с ним из Изумрудного города в Солнечный выехал на велосипеде почтальон Печкин. Их встреча произошла в 1 км от Солнечного города. Если бы расстояние между городами было на 2 км больше, то их встреча произошла бы в 1,5 км от Солнечного города. Во сколько раз скорость почтальона Печкина больше скорости Василия Ивановича?
Задача 7.
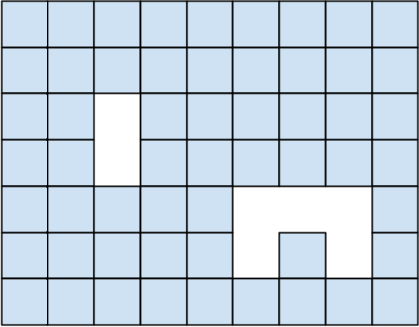
Из прямоугольника 7 × 9 вырезан прямоугольник 1 × 2 и фигура пентамино как показано на рисунке. Разрежьте получившуюся фигуру по линиям сетки на две одинаковые фигуры. (Напоминаем, что фигуры называются одинаковыми, если они совпадают при наложении!)
Задача 8.
На острове лжецов и рыцарей ровно один житель сказал: «Есть лжец выше меня», ровно двое жителей сказали: «Есть хотя бы двое лжецов выше меня», . . . , ровно 10 жителей сказали: «Есть хотя бы 10 лжецов выше меня». Известно, что все островитяне — разного роста, и каждый житель высказался ровно один раз. Сколько лжецов живёт на острове? (Рыцари — это те, кто всегда говорит правду, а лжецы — это те, кто всегда лгут.)

