Задача 1.
В рыбалке участвовали 7 рыбаков. Любые двое из них поймали различное количество рыбок. Кроме того, оказалось, что любые трое из них поймали вместе не менее 13 рыбок. Какое наименьшее число рыбок могли в сумме поймать все семеро рыбаков?
Задача 2.
Есть 4 монеты. Некоторые из них настоящие, некоторые фальшивые. Настоящие весят одинаково, фальшивые одинаково, настоящие тяжелее фальшивых. Есть двухчашечные весы без гирь. В весах живёт Весёлый Гнум. Каждый раз перед тем, как весы покажут результат взвешивания, он одну из монет (может даже которая не на чашах весов) меняет (то есть из фальшивой превращает в настоящую, из настоящей превращает в фальшивую). Но он никогда не делает так, что все монеты станут фальшивыми. Нужно найти хотя бы одну настоящую монету. Можно ли это сделать?
Задача 3.
Имеется клетчатая полоска 1 × 𝑁. В каждую клетку надо вписать одну из трёх цифр 1, 2, 3 так, чтобы для любой клетки, в которой записана цифра 1, нашлась клетка ровно через одну клетку от неё, в которой записана цифра 2; для каждой клетки, в которой записана цифра 2, нашлась клетка ровно через две клетки от неё, в которой записана цифра 3; а для каждой клетки, в которой записана цифра 3, нашлась клетка, ровно через три клетки от неё, в которой записана цифра 1. Докажите, что это можно сделать для любых 𝑁 больших 15.
Задача 4.
В понедельник Кузя шёл в школу со скоростью 6 км/ч и опоздал на 2 минуты. Во вторник он бежал со скоростью 10 км/ч и успел вовремя. На сколько он опоздает в среду, если будет идти со скоростью 4 км/ч?
Задача 5.
В кемпинг заехали туристы. На обед каждый из них съел половину банки супа, треть банки тушенки и четверть банки фасоли. Всего они съели 156 банок еды. Сколько было туристов?
Задача 6.
2019 человек, каждый из которых — рыцарь, всегда говорящий правду, или лжец, который всегда лжёт, выстроились в шеренгу. Затем каждый из них сказал: «Количество лжецов слева от меня больше, чем количество рыцарей справа от меня». Сколько в этой шеренге лжецов?
Задача 7.
На головах четырехглавого дракона однажды утром выросли волосы: на первой голове 100 волос, на второй — 5, на третьей — 28, на четвёртой — 39 (до этого утра ни на одной из голов никаких волос не было). За один раз дракон может вырвать три волоса с любой своей головы, но тогда на трёх других головах вырастает по одному волосу. Дракон хочет сделать, чтобы на всех головах оказалось одинаковое количество волос. Сможет ли он это сделать?
Задача 8.
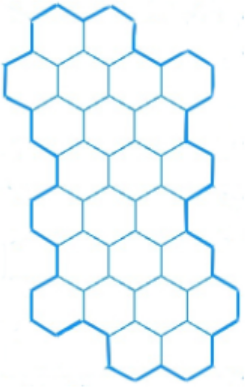
Разрежьте фигуру, изображённую на рисунке, на четыре равные части. Резать можно только по линиям сетки.