Задача 1.
Разрежьте фигуру, изображённую на рисунке, на три одинаковые части. Резать можно только по линям сетки.
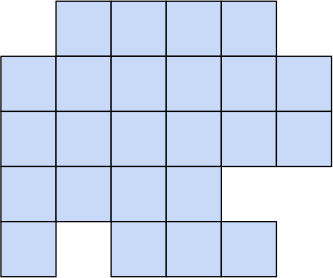
Задача 2.
Поезд проезжает мост, который в 6 раз длиннее его, за 112 секунд. За какое время проедет этот мост поезд, который в два раза длиннее, но едет со скоростью в два раза больше?
Задача 3.
В строку выписаны целые числа. Известно, что каждое число, начиная с третьего, равно сумме двух предшествующих, и двадцатое число равно 2019. Может ли оказаться, что сороковое число равно 20202020?
Задача 4.
В классе поровну мальчиков и девочек, всего 24 человека. Каждый мальчик написал, сколько в классе девочек выше его, а каждая девочка написала, сколько в классе мальчиков ниже её. Оказалось, что все написанные числа не меньше четверти числа учеников в классе. Докажите, что суммарный рост девочек в классе больше суммарного роста мальчиков.
Задача 5.
На острове живёт 29 рыцарей и лжецов. В утро вторника они произнесли следующие фразы:
- первый — «Среди нас можно выбрать группу из двух людей, среди которых лжецов будет больше, чем рыцарей»,
- второй — «Среди нас можно выбрать группу из трёх людей, среди которых лжецов будет больше, чем рыцарей»,
- . . . ,
- двадцать шестой — «Среди нас можно выбрать группу из 27 людей, среди которых лжецов будет больше, чем рыцарей».
- А трое промолчали.
Сколько рыцарей может быть среди них? (Рыцари всегда говорят правду, лжецы всегда врут.)
Задача 6.
У визиря Альмара в молодильных яблоках завёлся червячок. Всего яблок у него 9 и лежат они по кругу в специальной коробке Для-Молодильных-Яблок. Чтобы его найти Альмар решил воспользоваться чашечными весами. Он знает, что все яблоки весят одинаково, но то яблоко, в котором сейчас находится червячок, тяжелее. Есть небольшая проблема, связанная с тем, что после каждого взвешивания яблоки надо возвращать обратно в коробку, каждое на то самое место, на котором оно до этого и лежало. А после того, как Альмар возвращает яблоки в коробку, червячок сразу же незаметно переползает в одно из двух соседних с ним яблок (и живёт там до следующего взвешивания). Помогите визирю Альмару найти червивое яблоко.
Задача 7.
Костя решил придумать число, в котором все цифры различны, при этом соседние цифры отличаются не меньше, чем на 5. У него получилось число 27093. А каково наибольшее число с таким свойством?
Задача 8.
Квадрат разрезан на меньшие, не обязательно равные, квадраты с целыми периметром. Докажите, что периметр исходного квадрата — также целое число.

