Задача 1.
Клетки таблицы 4 × 4 раскрашены в пять цветов так, что в каждой строке, каждом столбце и каждом квадрате 2 × 2 все цвета различны. Известно, что один из этих цветов — персиковый. Какое наименьшее количество клеток персикового цвета может быть в таблице?
Задача 2.
На острове лжецов и рыцарей ровно один житель сказал: «Есть лжец выше меня», ровно двое жителей сказали: «Есть хотя бы двое лжецов выше меня», . . . , ровно 20 жителей сказали: «Есть хотя бы 20 лжецов выше меня». Известно, что все островитяне — разного роста, и каждый житель высказался ровно один раз. Сколько лжецов живёт на острове? (Рыцари — это те, кто всегда говорит правду, а лжецы — это те, кто всегда лгут.)
Задача 3.
Имеется 48 шариков: красные, синие, жёлтые, зелёные, фиолетовые. Может ли оказаться, что их можно разложить на 3 кучки так, что в каждой синих будет больше, чем красных; можно разложить на 4 кучки так, что в каждой жёлтых будет больше, чем синих; можно разложить на 6 кучек так, что в каждой зелёных будет больше, чем жёлтых и можно разложить на 8 кучек так, что фиолетовых будет больше, чем зелёных?
Задача 4.
Каждый ученик 6«Ы» класса посещает не более двух кружков. При этом для каждых двух учеников есть кружок, в который ходят они оба. Докажите, что есть кружок, в который ходит не менее двух третей всех учеников класса.
Задача 5.
Дан квадрат и несколько прямоугольников. Известно, что все стороны прямоугольников меньше стороны квадрата, а сумма периметров всех прямоугольников меньше периметра квадрата. Докажите, что все прямоугольники можно уложить в квадрат без наложений.
Задача 6.
Из Солнечного города в Изумрудный вышел Василий Иванович. Одновременно с ним из Изумрудного города в Солнечный выехал на велосипеде почтальон Печкин. Их встреча произошла в 1 км от Солнечного города. Если бы расстояние между городами было на 2 км больше, то их встреча произошла бы в 1,5 км от Солнечного города. Во сколько раз скорость почтальона Печкина больше скорости Василия Ивановича?
Задача 7.
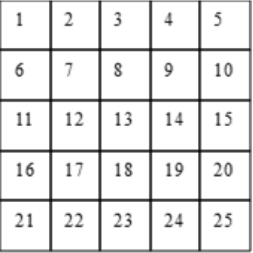
На клетках доски 5 × 5 лежат монетки (см. рисунок, число в клетке равно количеству монеток в данной клетке). Разрешается переложить одну монетку из одной клетки на соседнюю клетку по стороне, если в ней (в клетке, куда хотим переложить монетку) сейчас находится нечётное количество монеток. Так же можно к двум соседним по стороне клеткам доложить по одной монетке из мешка (в мешке имеется достаточно много монет). Можно ли при помощи таких операций сделать так, чтобы во всех клетках стало по 15 монет?
Задача 8.
У Афони есть шесть стаканов с чаем. Он может выбрать любые три стакана и перелить из них в три других стакана одинаковое количество чая (сколько переливать, Афоня каждый раз решает заново). Как ему добиться того, чтобы во всех стаканах чая стало поровну?

