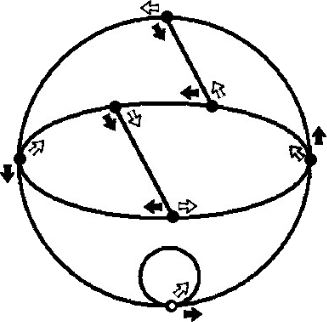
Дано натуральное число 𝑛. В белой точке внизу приложенного рисунка стоит фишка. Игрок читает первую (самую левую) цифру числа 𝑛 и делает фишкой столько ходов по чёрным стрелкам, сколько единиц в этой цифре. Если дальше есть вторая цифра, он двигает фишку по белой стрелке, а затем делает столько ходов по чёрным стрелкам, сколько единиц во второй цифре. Так он перебирает все цифры числа 𝑛: перед каждой новой цифрой двигает фишку по белой стрелке, а затем делает столько ходов по чёрным стрелкам, сколько единиц содержится в очередной цифре. (Например, при 𝑛 = 325 игрок идёт вдоль 3 чёрных стрелок, 1 белой, 2 чёрных, 1 белой и 5 чёрных.) Докажите, что если 𝑛 делится на 7, то фишка закончит свой маршрут в белой точке.