Задача 1.
В классе поровну мальчиков и девочек. Каждый мальчик написал, сколько в классе девочек выше его, а каждая девочка написала, сколько в классе мальчиков ниже её. Оказалось, что все написанные числа не меньше четверти числа учеников в классе. Докажите, что суммарный рост девочек в классе больше суммарного роста мальчиков.
Задача 2.
В строку выписаны целые числа. Известно, что каждое число, начиная с третьего, равно сумме двух предшествующих, и двадцатое число равно 2019. Может ли оказаться, что сороковое число равно 20202020?
Задача 3.
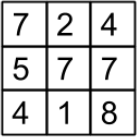
Таблица 3 × 3 заполнена числами, как показано на рисунке. Разрешается поменять местами числа в любых двух клетках, имеющих общую сторону. Можно ли, действуя таким образом, добиться того, чтобы сумма чисел в каждой строке и в каждом столбце делилась на 3?
Задача 4.
Квадрат разрезан на меньшие, не обязательно равные, квадраты с целыми периметром. Докажите, что периметр исходного квадрата — также целое число.
Задача 5.
300 человек играли между собой в пинг-понг. Каждые два человека сыграли между собой не более одного раза. При каком наибольшем 𝑛 могло случиться, что никто не сыграл больше 𝑛 партий, но были люди, сыгравшие все количества партий от 1 до 𝑛?
Задача 6.
Вдоль тропинки расположены 2019 норок, в одной из которых прячется мышонок Дуду. Кот Пажо может сунуть лапу в любую из норок; если Дуду в этой норке, Пажо его съест, а если нет, Дуду перебежит в норку, соседнюю (слева или справа) с той, в которой он сейчас. Может ли Пажо гарантированно съесть Дуду?
Задача 7.
У числового автомата есть четыре кнопки, нажатие на которые позволяет превратить введённое число 𝑛 в числа 2𝑛, 𝑛/2, 3𝑛+1, (𝑛−1)/3 соответственно. Докажите, что из любого натурального числа можно, нажимая на эти кнопки, получить число 1. (Не требуется, чтобы все промежуточные числа были натуральными.)
Задача 8.
Найдите наибольшее натуральное число, у которого все цифры различны и разность каждых двух соседних цифр не меньше 5.

