Задача 1.
Сколько существует пар натуральных чисел 𝑥 и 𝑦, для которых 200𝑥 + 4𝑦 = 2020?
Задача 2.
В однокруговом шахматном турнире Петя набрал в 10 раз больше очков, чем Вася. При каком наименьшем количестве участников турнира такое могло быть? (Победа – 1 очко, ничья – 1/2 очка, поражение – 0 очков.)
Задача 3.
За круглым столом сидят 2018 человек. Каждый из них – либо из клана рыцарей, всегда говорящих правду, либо из клана лжецов, которые всегда лгут. Каждый из сидящих заявил: «Оба моих соседа — из одного клана». Сколько рыцарей могло быть за столом (перечислите все возможности)?
Задача 4.
Одно положительное число поделили на другое. Найдите частное, если известно, что оно в 8 раз меньше делителя и в 4 раза больше делимого.
Задача 5.
На плоскости провели 9 прямых. Какое наибольшее число квадратов могло при этом образоваться?
Задача 6.
На доске надо записать несколько двузначных чисел так, чтобы их произведение делилось на все простые числа от 2 до 17. Каким наименьшим числом различных цифр можно для этого обойтись?
Задача 7.
Когда у прямоугольника площадью 36 см2 одну из сторон удлинили на 1 см, а другую — укоротили на 1 см, его площадь уменьшилась на 1 см2. Какими могли быть стороны исходного прямоугольника?
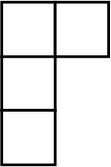
Задача 8.
К четырёхклеточной фигуре, имеющей форму буквы Г, требуется добавить ещё одну клетку так, чтобы получилась фигура, имеющая ось симметрии. Сколькими способами это можно сделать?