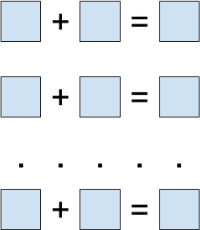
Задача 1.
Вокруг большой лужи встали 20 жителей острова рыцарей и лжецов (рыцари всегда говорят правду, лжецы всегда лгут) и посмотрели на неё. Потом каждый из 20 людей грустно сказал: «Среди следующих трёх людей справа от меня по кругу есть хотя бы 2 рыцаря». Сколько среди них было рыцарей?
Задача 2.
Какое наибольшее количество шестиклеточных сапожков можно вырезать из клетчатого прямоугольника 7 × 12?

Задача 3.
В наличии имеется мягкая верёвка длиной 1 метр и деревянная палочка длиной 7 см. Докажите, что с помощью этих инструментов можно отмерить любую длину от 11 до 17 см, выраженную целым числом сантиметров.
Задача 4.
Доску 11 × 11 заполняют числами от 1 до 121 по следующему правилу: в первой строке слева направо записаны числа от 1 до 11 в порядке возрастания, во второй — слева направо от 12 до 22 в том же порядке, и так далее. Может ли сумма в клетках, образующих Z-тетрамино, быть равной 244? (Z-тетрамино можно как угодно поворачивать и переворачивать.)
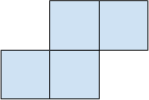
Задача 5.
Может ли произведение нескольких (больше одного) последовательных натуральных чисел быть равно 99 . . . 992 (2019 девяток и 1 двойка)?
Задача 6.
2019 детей встали в хоровод, каждый из них был в кепке одного из трёх цветов: белого, синего или красного. Неожиданно прибежали несколько котят и сели между детьми таким образом: если рядом стояли двое детей в кепках разных цветов, то между ними сели 1, 2 или 3 котёнка (1 котёнок между детьми в белой и синей кепках, 2 котёнка между детьми в красной и синей кепках, 3 котёнка между детьми в белой и красной кепках). Между парами детей в одноцветных кепках котята не сели. Могло ли всего между детьми сесть 2019 котят?
Задача 7.
Иннокентий придумал числовой ребус: АЛЬФА + АЛЕФ = ФИЛИН (Одинаковыми буквами заменены одинаковые цифры, разными — разные.) Найдите все решения ребуса и объясните, почему других решений нет.
Задача 8.
На доске написано 𝑁 примеров на сложение двух чисел. Двое играют в игру: каждым ходом в один из свободных квадратиков разрешается вписать любое натуральное число или 0. Когда все 3𝑁 чисел вписаны (во всех 𝑁 примерах вписаны оба слагаемых и сумма), игроки выясняют, сколько примеров на доске являются верными. Если хотя бы один пример верен, то выигрывает второй игрок, иначе выигрывает первый игрок. При каких значениях 𝑁 второй игрок может гарантировать себе победу вне зависимости от действий первого игрока?