Осенний математический Турнир Мёбиуса, 6 класс, 2019 год, высшая лига, 3 тур
дата проведения: 19 ноября 2019
Задача 1.
В строку выписаны целые числа. Известно, что каждое число, начиная с третьего, равно сумме двух предшествующих, и сотое число равно 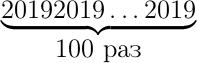 . Может ли оказаться, что двухсотое число равно
. Может ли оказаться, что двухсотое число равно 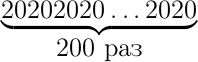 ?
?
Задача 2.
На свободные поля шахматной доски 8 × 8 по одному ставят чёрных и белых слонов. Чёрного слона можно поставить на свободное поле, если он бьёт чётное количество ранее выставленных слонов любого цвета (например, не бьёт ни одного слона), а белого — если он бьёт нечётное количество ранее выставленных слонов любого цвета. Таким образом заполнили все клетки доски. Какое наименьшее количество чёрных слонов могло при этом оказаться на доске?

