Задача 1.
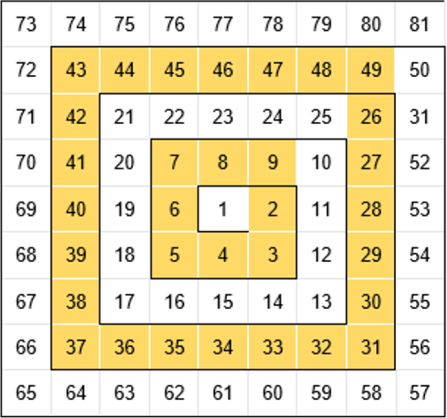
Числа натурального ряда записаны на клетчатой бумаге в форме спирали: в одной из клеток записано число 1, справа от неё в соседней клетке записано число 2, вниз от неё в соседней клетке записано число 3, и так далее: при движении по часовой стрелке по спирали читается натуральный ряд. Рассмотрим квадрат 21 × 21, в центре которого стоит число 1. Найдите сумму чисел, стоящих на периметре этого квадрата.
Задача 2.
Есть 7 монет: 4 настоящие и 3 фальшивые. Настоящие монеты весят одинаково, фальшивые тоже одинаково, но вес фальшивой отличается от веса настоящей. По внешнему виду монеты не различаются. Как за 4 взвешивания на чашечных весах без гирь определить какая монета тяжелее: настоящая или фальшивая?
Задача 3.
Коля нарисовал клетчатый квадрат 10 × 10 и вырезал из него 6 клеток. Оказалось, что вырезанные клетки не имеют общих точек и не примыкают к сторонам исходного квадрата. Пришел Никита, посмотрел на получившуюся фигуру и сказал, что из неё можно вырезать уголок из трёх клеток 𝑛 способами. Чему может быть равно 𝑛?
Задача 4.
Аня и Боря вышли одновременно из пунктов А и Б навстречу друг другу и встретились через 30 минут. В этот момент из А вышел Артур и через 15 минут встретился с Борей на середине пути. На сколько минут Аня пришла в Б раньше Артура?
Задача 5.
Возрастающая последовательность 𝑎1 < 𝑎2 < . . . < 𝑎100 натуральных чисел такова, что все суммы 𝑎1 + 𝑎100 , 𝑎2 + 𝑎99 , . . . , 𝑎50 + 𝑎51 различны. При каком наименьшем значении 𝑎100 это возможно?
Задача 6.
Натуральные числа 𝑎, 𝑏, 𝑐, 𝑑 удовлетворяют условию 𝑎 + 𝑏 + 𝑐 + 𝑑 = (𝑎 − 𝑏)(𝑏 − 𝑐)(𝑐 − 𝑑)(𝑑 − 𝑎). Докажите, что сумма 𝑎 + 𝑏 + 𝑐 + 𝑑 делится на 4.
Задача 7.
В каждой клетке бесконечного клетчатого поля стоит рыцарь или лжец, причём все смотрят в одну сторону. Может ли оказаться, что каждый из них может произнести четыре фразы: «У моего соседа спереди не менее двух соседей являются рыцарями», «У моего соседа справа не менее двух соседей являются рыцарями», «У моего соседа сзади не менее двух соседей являются лжецами», «У моего соседа слева не менее двух соседей являются лжецами»?
Задача 8.
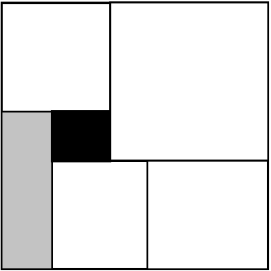
Квадрат разрезали на 5 квадратов и 1 прямоугольник (прямоугольник закрашен серым цветом). Какую часть площади исходного квадрата занимает чёрный квадрат?