Задача 1.
Несколько подряд идущих натуральных чисел расставлено по двум кругам так, что сумма любых двух соседних чисел в любом круге кратна 3. В одном из кругов стоит 2021 число. Сколько чисел может быть в другом круге? (Круги не имеют общих чисел.)
Задача 2.
Клетки некоторой клетчатой фигуры на плоскости раскрашены в красный, жёлтый и зелёный цвета так, что любые две клетки, имеющие общую сторону, разного цвета. Эту фигуру двумя способами разбили на доминошки (прямоугольники 1 × 2). Докажите, что количество доминошек, у которых одна клетка красная, а другая зелёная, в этих способах одинаково.
Задача 3.
Имеется белый квадрат 8 × 8 клеток. Костя и Никита по очереди закрашивают клетки. Начинает Костя. За один ход можно закрасить чёрным цветом любую белую клетку. Тот, после хода которого на доске не останется двух рядом стоящих белых клеток — выигрывает. Кто выигрывает при правильной игре?
Задача 4.
В числе переставили цифры. Могло ли оно увеличиться более, чем в 9 раз?
Задача 5.
У Люды есть восемь золотых шариков: четыре по 51 грамму и четыре по 52 грамма. Все шарики выглядят одинаково и на ощупь неразличимы. Люда не помнит, какой из них есть какой. Ей нужно разделить шарики на две кучки одинаковой массы. В распоряжении Люды есть электронные весы, которые показывают вес груза, который на них положили. Но в весах практически села батарейка, и поэтому их может хватить только на 2 взвешивания. Помогите Люде справиться с задачей.
Задача 6.
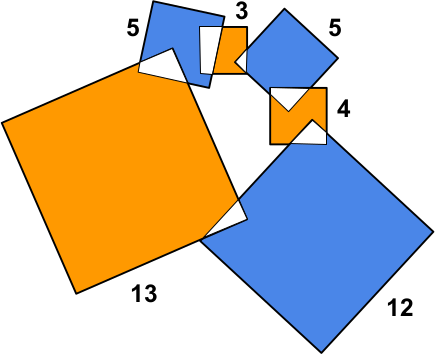
Люда нарисовала шесть квадратов так, как показано на рисунке. Длины сторон квадратов равны 3, 5, 4, 12, 13, 5. Чему может быть равна разность площадей синих и оранжевых частей?
Задача 7.
Числа от 1 до 101 выписаны на доске в строчку (не обязательно по порядку). Вася написал в тетради 101 число: первое выписанное на доске число, сумму первых двух выписанных на доске чисел, сумму первых трёх чисел, . . . , сумму всех чисел. Коля тоже написал в тетради 101 число: последнее выписанное на доске число, сумму двух последних выписанных на доске чисел, сумму последних трёх чисел, . . . , сумму всех чисел. У Васи получилось 39 нечётных чисел. Сколько нечётных чисел получилось у Коли?
Задача 8.
В клетках таблицы 3 × 3 слева направо в первой строке записаны числа 1, 2, 3, во второй строке записаны слева направо числа 4, 5, 6, в третьей строке — слева направо числа 7, 8, 9. За один ход разрешается выбрать в этой таблице произвольный квадратик 2 × 2 и увеличить в нём некоторые два числа, стоящие по диагонали, на 1, а два других числа, — уменьшить на 1. Можно ли при помощи таких ходов сделать не менее 6-ти чисел равными?

