Задача 1.
На доске написаны четыре двузначных числа. Оказалось, что сумма тех из них, в записи которых есть цифра 2, равна 80. Сумма тех из них, в записи которых есть цифра 3, равна 90. Сумма тех из них, в записи которых есть цифра 5, равна 60. Какие четыре числа могли быть записаны на доске? Приведите все возможные варианты и докажите, что других нет!
Задача 2.
Имеется полоска 1 × 2021. Арним и Брентано играют в следующую игру. Сперва Арним ставит в одну из клеток фишку. Каждым ходом Брентано называет натуральное число 𝑘, которое не превосходит 1011, а Арним сдвигает фишку на 𝑘 клеток в любую сторону по своему выбору. Докажите, что Брентано может действовать так, чтобы при любых действиях Арнима фишка вышла за пределы полосы.
Задача 3.
Можно ли так расставить в клетках таблицы 2×3 различные натуральные числа, чтобы сумма чисел в любой строке и в любом столбце являлась бы простым числом? Напомним, что простым называется натуральное число, которое имеет ровно два натуральных делителя — единицу и само себя.
Задача 4.
Бабушка испекла для привередливого внучка 11 пирожков и выложила их в ряд, сообщив внуку, что 5 пирожков его любимые — с вишней, а остальные 6 — с любимой бабушкиной смесью «брокколи-шпинат-сельдерей», которые внучок считает отвратительными. Еще она сообщила, что пирожки с вишней лежат так, что рядом с любым вишневым есть ещё один вишнёвый. Какое наименьшее количество пирожков должен съесть мальчик, чтобы среди них гарантированно нашёлся вишнёвый пирожок?
Задача 5.
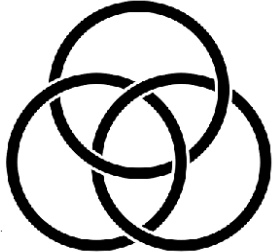
Кольца Борромео образуют на плоскости 7 зон. Можно ли расставить в этих зонах числа от 1 до 7 так, чтобы сумма чисел в каждом из колец была бы одна и та же?
Задача 6.
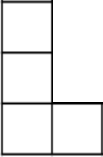
При каком наименьшем значении 𝑆 существует фигура из 𝑆 клеток, которую можно разрезать на фигурки 𝐿–тетрамино несколькими разными способами?
Задача 7.
В банке сидят 50 синих и 50 красных бактерий. Каждую секунду одна из бактерий делится. При этом синяя бактерия делится на две красные, а красная — на три синие. Через минуту в банке оказалось 200 бактерий. Сколько среди них синих и сколько красных?
Задача 8.
По кругу стояло несколько людей, каждый из них был рыцарем или лжецом. Каждый человек в круге заявил: «Среди следующих трёх людей от меня по часовой стрелке есть хотя бы 1 лжец». Сколько людей могло быть в этом круге?

