Задача 1.
На доске написаны 5 различных натуральных чисел. Известно, что сумма любых трёх из них больше суммы остальных двух. Какое наименьшее число может встретиться на доске?
Задача 2.
Есть доска 8 × 8. В половине её клеток не нарисовано ничего, а в каждой из оставшихся нарисована одна из следующих картинок:
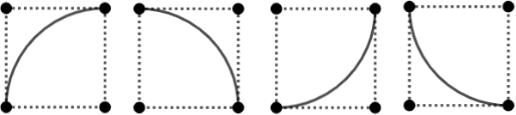
Может ли оказаться, что все нарисованные дуги образуют замкнутую гладкую несамопересекающуюся кривую?
Задача 3.
Матвей придумал ребус КУСТ + ПЕНЬ = АААА. (Одинаковыми буквами заменены одинаковые цифры, разными — разные.) Верно ли, что А равно 9?
Задача 4.
Три человека давали друг другу советы. Первый и второй в общей сложности дали на 17 советов больше, чем третий. Могло ли оказаться, что второй и третий дали в общей сложности на 14 советов больше, чем первый?
Задача 5.
Аня и Боря играют в игру, делая по очереди ходы на следующей доске: Каждым своим ходом Аня ставит единицу в одну из свободных клеток, рядом с которой уже стоит единица. Каждым своим ходом Боря ставит двойку в одну из свободных клеток, рядом с которой уже стоит двойка. Проигрывает тот, кто поставит свою цифру в центральную клетку. Кто выиграет при правильной игре: Аня или Боря?
Задача 6.
По кругу лежат 6 монет, среди них 4 настоящих, они весят одинаково, фальшивые монеты тоже весят одинаково, причём фальшивая монета весит легче настоящей. Можно ли за 1 взвешивание на чашечных весах без гирь найти хотя бы 1 фальшивую монету, если дополнительно известно, что фальшивые монеты лежат рядом?
Задача 7.
Есть две корзины, в одной из которых лежат синие шарики, а в другой — зелёные. Паша и Витя решили перенести все синие шарики во вторую корзину, а все зелёные — в первую. Паша брал несколько синих шариков из первой корзины, переносил их во вторую корзину, а оттуда брал количество зелёных шариков, отличающееся в 3 раза, и нёс их обратно в первую корзину. Витя брал несколько зелёных шариков из второй корзины, переносил их в первую корзину, а оттуда брал количество синих шариков, отличающееся в 7 раз, и нёс их обратно во вторую корзину. В итоге они все шарики поменяли местами. Могло в корзинах быть по 707 шариков?
Задача 8.
Восемь друзей: Абель, Бернулли, Вейерштрасс, Гаусс, Декарт, Евклид, Жордан и Зигмонди купили билеты в кино на восемь последовательных мест в одном ряду. Известно, что:
- Бернулли сел на указанное в своём билете место;
- Вейерштрасс сел на место, которое на два правее, чем указанное в билете Жордана;
- Гаусс сел на место, которое на один левее, чем указанное в билете Евклида;
- Декарт сел на место, которое на четыре левее, чем указанное в билете Зигмонди;
- Евклид сел на место, которое на пять правее, чем указанное в билете Гаусса;
- Жордан сел на место, которое на один правее, чем указанное в билете Декарта;
- Зигмонди сел на место, которое на три места левее, чем указанное в билете Абеля.
На чьё место сел Абель?

