Задача 1.
На огороде растёт капуста. В первый день Костя собрал несколько кочанов, а в каждый следующий день он собирал в два раза больше кочанов, чем в предыдущий. Известно, что в пятый день Костя собрал на 100 кочанов больше, чем во второй и в третий дни вместе. Сколько кочанов Костя собрал в первый день?
Задача 2.
Вася взял шесть карточек и пронумеровал числами от 1 до 6. Затем он перемешал карточки, выложил в ряд в некотором порядке, каждую карточку перевернул и на обратных сторонах карточек написал следующие верные утверждения.
- На первой карточке: «Число на этой карточке нечётно».
- На второй: «Число на этой карточке меньше каждого из чисел на соседних карточках».
- На третьей: «Число на этой карточке больше 4».
- На четвёртой: «Число на этой карточке делится на 3».
- На пятой: «Число на этой карточке равно сумме чисел, написанных на соседних карточках».
- На шестой: «На этой карточке написано моё любимое число».
Определите, в каком порядке лежат карточки.
Задача 3.
Вася покатался на лифте в 21-этажном доме, и теперь в этом лифте работают только четыре кнопки: «+3», «−3», «+5», «−5» (при нажатии на которые лифт едет соответственно на три этажа вверх, на три этажа вниз, на пять этажей вверх и на пять этажей вниз). Водопроводчик Степан находится на первом этаже и хочет объехать все остальные. Как ему это сделать, нажав на кнопку не более 22 раз?
Задача 4.
Клетки доски 2021 × 2022 раскрашены в шахматном порядке. Можно ли положить на эту доску несколько доминошек так, чтобы каждая белая клетка была накрыта ровно двумя доминошками, а каждая чёрная — ровно одной или ровно трёмя?
Задача 5.
Имеется 8 ключей, из которых четыре — волшебные. В замок волшебного сейфа можно вставить любое число ключей, но чтобы замок открылся, волшебными должны быть ровно два ключа из вставленных. Покажите, как открыть сейф за три попытки.
Задача 6.
Антонио, Борисио и Вованио загадали по одному натуральному числу. Одно из чисел оказалось пятизначным, другое четырёхзначным, а третье – трёхзначным. Число Борисио было в 24 раза больше числа Антонио. Кроме того, в числе Вованио было как минимум 4 нечётных цифры, а также оно было равно сумме чисел Борисио и Антонио. Какое число мог загадать Вованио?
Задача 7.
Дан куб 5 × 5 × 5. Из него нужно по клеточкам вырезать одну фигурку такого вида (рисунок ниже). Сколькими способами это можно сделать?
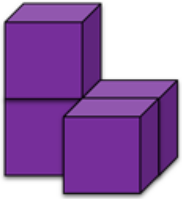
Задача 8.
В левой нижней клетке таблицы 9 × 9 сидели несколько чёрных сусликов, а в левой верхней — несколько белых сусликов. За один ход каждый чёрный суслик может перебежать в клетку, примыкающую к его клетке справа или сверху, а каждый белый — в клетку, примыкающую к его клетке справа или снизу. После некоторого количества ходов оказалось, что суслики побывали во всех клетках. Какое наименьшее количество сусликов может быть в таблице?

