Дано натуральное число 𝑛. Имеется полоска 1 × 2021. Арним и Брентано играют в следующую игру. Сперва Арним ставит в одну из клеток фишку. Каждым ходом Брентано называет натуральное число 𝑘, которое не превосходит 𝑛, а Арним сдвигает фишку на 𝑘 клеток в любую сторону по своему выбору. Если при этом фишка выходит за пределы полосы, Брентано побеждает. При каком наименьшем значении 𝑛 Брентано может победить независимо от действий Арнима?

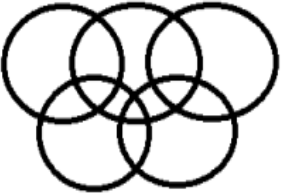
Олимпийские кольца образуют на плоскости 15 зон. Можно ли расставить в этих зонах числа от 1 до 15 так, чтобы сумма чисел в каждом из колец была бы одна и та же?

Поверхность куба 3 × 3 × 3 разбита на клеточки, в каждой из которых записано натуральное число. Для любой клетки Вася посчитал сумму чисел в этой клетке, а также во всех соседних с ней по стороне, и все полученные суммы записал на доску. В итоге на доске оказалось 18 раз записано число 101, 18 раз записано число 102 и 18 раз записано число 103. Докажите, что Вася по меньшей мере один раз ошибся.

По кругу стояло несколько людей, каждый из которых был рыцарем или лжецом. Каждый человек в круге сделал одно из двух заявлений: «Среди следующих двух людей от меня по часовой стрелке есть хотя бы 1 лжец» или «Среди следующих трёх людей от меня по часовой стрелке есть хотя бы 1 лжец». Сколько людей могло быть в этом круге? Приведите все варианты и докажите, что других нет!