Задача 1.
На доске написаны 11 различных натуральных чисел. Известно, что сумма любых шести из них больше суммы остальных пяти. Какое наименьшее число может встретиться на доске?
Задача 2.
Есть доска 8 × 8. В каждой её клетке либо не нарисовано ничего, либо нарисована одна из следующих картинок:
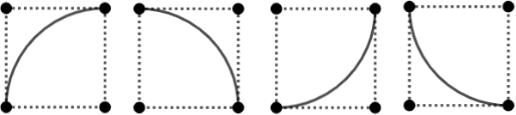
При этом все нарисованные дуги образуют замкнутую гладкую несамопересекающуюся кривую. Какое наибольшее число клеток может содержать дуги?
Задача 3.
Имеются две банки, в которых с утра плавали амёбы синего, зелёного, жёлтого и красного цветов, причём амёб каждого цвета в обеих банках поровну. В полдень все амёбы в банках разбились на пары так, что в каждой паре встретились амёбы разных цветов. После этого в каждой паре обе амёбы изменили цвета на те, которые до того в этой паре отсутствовали. Например, если в паре встретились зелёная и жёлтая амёбы, то они станут синей и красной амёбами. После полудня Дима посчитал число красных амёб в первой банке, а Никита — во второй. У Димы получилось 20, а у Никиты 21. Докажите, что по меньшей мере один из них ошибся.
Задача 4.
Из середины двух длинных сторон прямоугольника 5 × 12 вырезали по две клетки (таким образом, оставшаяся фигура состоит из двух квадратов 5 × 5 и соединяющего их прямоугольника 3 × 2). Докажите, что количество способов разрезать на доминошки оставшуюся фигуру является квадратом натурального числа. (Два разрезания считаются различными, если какие-то две клетки в одном из них принадлежат одной доминошке, а в другом — разным.)