Задача 1.
На доске написаны четыре двузначных числа. Оказалось, что сумма тех из них, в записи которых есть цифра 2, равна 80. Сумма тех из них, в записи которых есть цифра 3, равна 90. Сумма тех из них, в записи которых есть цифра 5, равна 60. Какие четыре числа могли быть записаны на доске? Приведите все возможные варианты и докажите, что других нет!
Задача 2.
В банке сидят 50 синих и 50 красных бактерий. Каждую секунду одна из бактерий делится. При этом синяя бактерия делится на две красные, а красная — на три синие. Через минуту в банке оказалось 200 бактерий. Сколько среди них синих и сколько красных?
Задача 3.
Бабушка испекла для привередливого внучка 11 пирожков и выложила их в ряд, сообщив внуку, что 5 пирожков его любимые — с вишней, а остальные 6 — с любимой бабушкиной смесью «брокколи-шпинат-сельдерей», которые внучок считает отвратительными. Еще она сообщила, что пирожки с вишней лежат так, что рядом с любым вишневым есть ещё один вишнёвый. Какое наименьшее количество пирожков должен съесть мальчик, чтобы среди них гарантированно нашёлся вишнёвый пирожок?
Задача 4.
По кругу стояло несколько людей, каждый из которых был рыцарем или лжецом. Каждый человек в круге сделал одно из двух заявлений: «Среди следующих двух людей от меня по часовой стрелке есть хотя бы 1 лжец» или «Среди следующих трёх людей от меня по часовой стрелке есть хотя бы 1 лжец». Сколько людей могло быть в этом круге? Приведите все варианты и докажите, что других нет!
Задача 5.
Можно ли так расставить в клетках таблицы 2 × 3 попарно различные натуральные числа так, чтобы сумма чисел в любой строке и в любом столбце являлась простым числом?
Задача 6.
Дано натуральное число 𝑛. Имеется полоска 1 × 2021. Арним и Брентано играют в следующую игру. Сперва Арним ставит в одну из клеток фишку. Каждым ходом Брентано называет натуральное число 𝑘, которое не превосходит 𝑛, а Арним сдвигает фишку на 𝑘 клеток в любую сторону по своему выбору. Если при этом фишка выходит за пределы полосы, Брентано побеждает. При каком наименьшем значении 𝑛 Брентано может победить независимо от действий Арнима?
Задача 7.
Каждые два города страны соединены прямым автобусным или авиасообщением.
- Клика — это набор городов, попарно соединённых авиарейсами.
- Клюка — это набор городов, попарно соединённых авиарейсами и при этом таких, что из них выходит одинаковое количество автобусных маршрутов.
- Кляка — это набор городов, попарно соединённых авиарейсами и при этом таких, что из любых двух из них выходит разное количество автобусных маршрутов.
Докажите, что количество городов в любой клике не превосходит произведения максимально возможного количества городов в клюке и максимально возможного количества городов в кляке.
Задача 8.
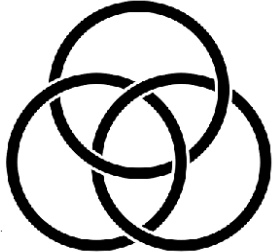
Кольца Борромео образуют на плоскости 7 зон. Можно ли расставить в этих зонах числа от 1 до 7 так, чтобы сумма чисел в каждом из колец была бы одна и та же?