Имеются две банки, в которых с утра плавали амёбы синего, зелёного, жёлтого и красного цветов, причём амёб каждого цвета в обеих банках поровну. В полдень все амёбы в банках разбились на пары так, что в каждой паре встретились амёбы разных цветов. После этого в каждой паре обе амёбы изменили цвета на те, которые до того в этой паре отсутствовали. Например, если в паре встретились зелёная и жёлтая амёбы, то они станут синей и красной амёбами. После полудня Дима посчитал число красных амёб в первой банке, а Никита — во второй. У Димы получилось 20, а у Никиты 21. Докажите, что по меньшей мере один из них ошибся.

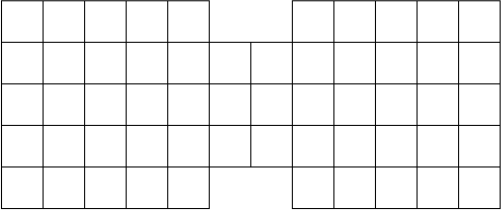
Из середины двух длинных сторон прямоугольника 5 × 12 вырезали по две клетки (таким образом, оставшаяся фигура состоит из двух квадратов 5 × 5 и соединяющего их прямоугольника 3 × 2). Докажите, что количество способов разрезать на доминошки оставшуюся фигуру является квадратом натурального числа. (Два разрезания считаются различными, если какие-то две клетки в одном из них принадлежат одной доминошке, а в другом — разным.)

По кругу лежат 6 монет, среди них 4 настоящих, они весят одинаково, фальшивые монеты тоже весят одинаково, причём фальшивая монета весит легче настоящей. Можно ли за 1 взвешивание на чашечных весах без гирь найти хотя бы 1 фальшивую монету, если дополнительно известно, что фальшивые монеты лежат рядом?

На складе имеется неограниченный запас пробирок трёх видов. Каждая пробирка содержит 1 г раствора сбрендинола: 10-процентного в пробирках красного цвета, 20-процентного в пробирках синего цвета и 90-процентного в пробирках белого цвета. Вася берёт пробирки по одной и выливает их содержимое в котёл (первоначально пустой). Две одноцветные пробирки подряд выливать в котёл нельзя. Какое наименьшее количество пробирок нужно вылить в котёл, чтобы получился раствор сбрендинола с концентрацией ровно 20,1%?

На доске написаны 7 различных натуральных чисел. Известно, что сумма любых четырёх из них больше суммы остальных трёх. Какое наименьшее число может встретиться на доске?

Антонио и Борисио играют в игру на доске 3 × 19 (3 строки, 19 столбцов), делая ходы по очереди. За один ход Антонио может вырезать по линиям сетки фигуру 2 × 1 или фигуру 1 × 2, а Борисио в свой ход может вырезать фигуру 1 × 3 или 3 × 1. Тот, кто не может сделать очередной ход, проигрывает. Кто выигрывает при правильной игре обоих игроков, если начинает Антонио?

Пять человек давали друг другу советы. Первый и второй в общей сложности дали на 17 советов больше, чем вместе третий, пятый и четвёртый. Могло ли оказаться, что второй и третий дали в общей сложности в 17 раз больше советов, чем первый, пятый и четвёртый вместе?

Вася приехал на поезде в «Зелёный Остров» и пытается открыть чемодан. Чемодан закрыт на кодовый замок. Кодовый замок состоит из пяти цилиндров, на каждом из которых по кругу стоят цифры от 0 до 9. Вася знает, что замок откроется, если на нём будет пять любых одинаковых цифр, но из-за холода Вася не может снимать перчатки и может поворачивать только два рядом стоящих цилиндра. Сможет ли он открыть замок?