Задача 1.
В задачнике с пожелтевшими страницами напечатано уравнение: 3 * 𝑦 * 2 = 𝐴. Вместо * стояли знаки действий, а вместо 𝐴 — некоторое число. Переписывая уравнение в тетрадь, Игорь и Игнат верно смогли разглядеть число (вместо буквы 𝐴), а вот вместо первой * Игорь поставил знак умножения, а Игнат поставил плюс, а вместо второй * Игорь увидел минус, а Игнат знак умножения. Тем не менее, решив уравнение, оба мальчика получили один и тот же ответ. Какое число было вместо числа 𝐴?
Задача 2.
Три аборигена, каждый из которых является либо рыцарем, либо лжецом, обнаружили в пещере на стене написанные два натуральных числа.
- Первый сказал: «Их сумма равна 49. Их разность равна 16».
- Второй сказал: «Их сумма равна 49. Их разность равна 13».
- Третий сказал: «Да вы оба лжецы. Сумма чисел равна 80. Разность чисел равна 54».
Найдите эти числа.
Задача 3.
Антон умножил некоторое число на количество цифр в этом числе. Борис сделал то же самое с другим числом. Могли ли у них получиться одинаковые результаты?
Задача 4.
Разрежьте данную фигуру на две равные части. Части можно поворачивать и переворачивать.
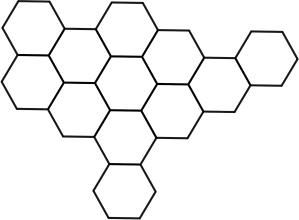
Задача 5.
У Коли есть 5 гирь весом 2, 3, 4, 5, 6 граммов. Он хочет добавить к ним ещё одну, чтобы полученные 6 гирь можно было разбить на три группы одинаковой массы. Можно ли добавить гирю массой больше 7 граммов?
Задача 6.
Лёня и Мотя одновременно вышли навстречу друг другу, встретились они через полчаса на середине пути. На следующий день они решили поехать на велосипедах и снова встретились посередине, но уже через 15 минут после старта. А сколько времени пройдёт до их встречи, если только Мотя поедет на велосипеде, а Лёня пойдёт пешком? (Все скорости постоянны. Скорость Лёни пешком и скорость Моти на велосипеде во все дни одинаковые.)
Задача 7.
Художник Антон рисует картину (см. рисунок), после чего ставит в каждой области число 1, 2 или 3 так, что числа в областях, имеющих общий кусок границы, отличаются (ниже приведён один из возможных способов расстановки чисел на картине). Цена картины равна сумме изображённых на ней чисел. За какую наибольшую цену Антон может продать картину?
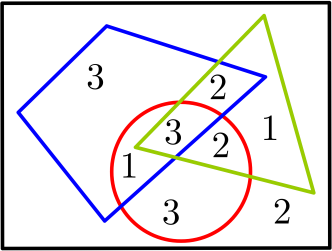
Задача 8.
В клетках доски 3 × 3 лежат монеты, в каждой клетке ровно одна. Шесть из них настоящие, а три фальшивые, которые легче настоящих. Фальшивые монеты весят одинаково и настоящие монеты весят одинаково. Также известно, что все фальшивые монеты лежат в одном столбце или одной строке. Внешне монеты не различимы. Как за два взвешивания на двухчашечных весах без гирь найти все фальшивые монеты?

