Задача 1.
В таблице 4 × 4 расставлены натуральные числа. Назовем число хорошим, если оно равно разности каких-то двух чисел, которые стоят с ним рядом (два числа стоят рядом, если они находятся в соседних по стороне клетках). Какое наибольшее количество хороших чисел может оказаться в таблице?
Задача 2.
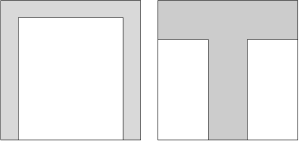
Художник, рисуя плакат, вписал в прямоугольник букву П толщиной 1 см (как на рисунке ниже). Периметр буквы П равен 42 см. Затем в такой же прямоугольник он вписал букву Т (толщина неизвестна, но у «шляпки» и у «ножки» одинакова) с периметром 28 см. Найдите длины сторон прямоугольника.
Задача 3.
Петя и Вася шли домой со школьного праздника с полными карманами конфет через Зачарованный лес. Когда один из них спотыкался на левую ногу, то он терял 2 конфеты, а другой находил 5 конфет; когда один спотыкался на правую ногу, то он терял 10 конфет, а другой находил 1 конфету; когда один падал, то он терял 13 конфет, а другой находил 7 конфет. Когда Петя и Вася добрались до дома, оказалось, что у Васи в два раза больше конфет, чем у Пети. Могло ли быть такое, что, когда Петя и Вася вышли из школы, у них в карманах было 47 и 54 конфеты?
Задача 4.
Дом имеет размеры 2 × 3 × 3 и состоит из 18 квартир (каждый кубик 1 × 1 × 1 – одна квартира). В каждой квартире живёт рыцарь, который всегда говорит правду, или лжец, который всегда врёт. Однажды каждый житель дома заявил: «Всего среди всех моих соседей по грани чётное число лжецов». Какое наибольшее количество лжецов может жить в этом доме?

