Задача 1.
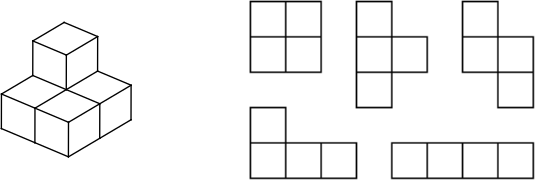
У Антона было пять единичных кубиков. Он склеил из них косую пирамидку (см. рисунок). Затем Антон вырезал из бумаги все пять различных тетрамино. Можно ли полученную фигуру из пяти кубиков оклеить пятью тетрамино в один слой? (Фигуры тетрамино можно переворачивать и сгибать по границам клеток.)
Задача 2.
Матбой длился более двух, но менее трёх часов. Саша записал в протоколе время его начала и время окончания (часы и минуты в 24-часовом формате) и обратил внимание, что числа, обозначающие часы и минуты, поменялись за время матбоя местами. Сколько мог длиться матбой с точностью до минуты?
Задача 3.
По кругу стоят 20 человек, каждый из которых — либо рыцарь, который всегда говорит правду, либо лжец, который всегда врёт. Для каждого из них три ближайших человека слева и три ближайших человека справа являются его друзьями, а остальные — нет. Каждый произнёс фразу: «Среди моих друзей есть по крайней мере два лжеца». Какое наибольшее количество лжецов может быть среди них?
Задача 4.
Докажите, что при каждом 𝑁 > 6 числа от 1 до 𝑁 можно расставить по кругу так, чтобы любые два соседних отличались либо на 1, либо на 4.
Задача 5.
Петя и Вася играют в такую игру. Каждым ходом игрок называет натуральное число, меньшее 40, не имеющее общих делителей, больших 1, ни с одним из ранее названных чисел. Ходы делаются по очереди, первым ходит Петя. Проигрывает тот, кто не сможет сделать ход. Кто из игроков имеет выигрышную стратегию?
Задача 6.
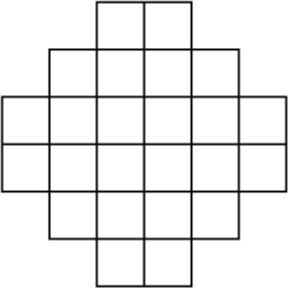
Фигура на рисунке состоит из квадратных клеток со стороной 1. Найдите наибольшую длину замкнутой ломаной без самопересечений, звенья которой совпадают со сторонами клеток.
Задача 7.
Костя загадал три попарно различных двузначных числа и сообщил их Свете. Света заметила, что если сложить эти числа и зачеркнуть старшую цифру в полученной сумме, то получится одно из первоначально загаданных Костей чисел. Сколько различных троек чисел мог загадать Костя? Считайте, что числа в тройке неупорядоченные, то есть тройки (10, 20, 30) и (30, 10, 20) считаются одинаковыми.
Задача 8.
Среди 11 одинаковых на вид монет 10 весят одинаково, а последняя отличается от них по весу. Можно ли за два взвешивания на чашечных весах определить, тяжелее эта монета остальных или легче?

