Задача 1.
Десять художников в футболках, на которых написаны числа от 1 до 10 (каждое число есть ровно на одной футболке), встали по кругу, причём художники в футболках, на которых написаны числа, отличающиеся на 1, не стоят рядом. Каждая футболка красного или синего цвета. Известно, что художники в красных футболках всегда врут, а художники в синих футболках всегда говорят правду.
- Художник в футболке с числом 1 сказал: «Рядом со мной по часовой стрелке стоит человек в красной футболке».
- Художник в футболке с числом 2 сказал: «Через одного человека от меня по часовой стрелке стоит человек в красной футболке».
- ...
- Художник в футболке с числом 9 сказал: «Через восемь человек от меня по часовой стрелке стоит человек в красной футболке».
- Художник в футболке с числом 10 не сказал ничего.
Какое наименьшее число художников может быть в красных футболках?
Задача 2.
Яблоко, груша и апельсин стоят дороже 11 копеек, а три яблока, три груши и апельсин стоят дешевле 27 копеек. Все фрукты стоят целое число копеек, фрукты одного вида стоят одинаково. Сколько стоит каждый фрукт, если груша самая дорогая?
Задача 3.
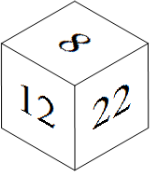
На каждой грани куба написано целое число. Три из них показаны на рисунке, а про остальные три известно, что они простые. Кроме того, суммы чисел на противоположных гранях равны. Чему может быть равна сумма всех чисел на кубе?
Задача 4.
Имеется набор гирь: пять гирь по 1 г, одна гиря в 2 г и одна гиря в 3 г. Внешне гири неразличимы. За два взвешивания на весах, показывающих массу положенных на них гирь, разбейте все гири на две кучки одинаковой массы.
Задача 5.
В некоторый прямоугольник можно поместить 100 кругов радиуса 2 без наложений. Докажите, что в него можно поместить 400 кругов радиуса 1 без наложений.
Задача 6.
На доске написаны три числа: 248, 482, 824. Двое играют в игру, делая ходы поочерёдно. За ход разрешается выбрать любое число на доске и разделить на любую его цифру, большую 1. При этом старое число с доски стирается, а новое число-частное записывается на доску. Например, если на доске написано число 1250, то его можно разделить на 2 или на 5, и вместо числа 1250 на доске появится число 625 или 250 соответственно. Тот, кто не может сделать очередной ход, проигрывает. Кто из игроков может обеспечить себе победу, вне зависимости от действий другого игрока?
Задача 7.
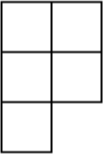
Имеется клетчатый прямоугольник 4 × 6. Какое наименьшее количество клеток нужно вырезать из этого прямоугольника, чтобы из оставшейся части нельзя было вырезать фигуру P-пентамино (см. рисунок)? При вырезании фигуру P-пентамино можно переворачивать и поворачивать.
Задача 8.
Из целого куска пластилина можно без остатка слепить либо пять больших миньонов, либо восемь средних, либо 20 маленьких. Из этого куска слепили двух больших миньонов и трёх средних. Сколько маленьких миньонов можно слепить из оставшегося пластилина?

