Задача 1.
Северный олень бежит по тундре со скоростью 30 км/ч, иногда он пугается и тогда следующие 10 минут бежит со скоростью в два раза большей. Если олень испуган, то дополнительно напугать его нельзя. Чукча заметил, что за 55 минут олень пробежал 40 км. Сколько раз олень пугался в течение этих 55 минут, если в самом начале он не был напуган?
Задача 2.
В 15-литровые вёдра налито соответственно 1, 2, 3, 4 и 5 литров воды. Разрешается перелить из любого ведра в любое другое вдвое больше воды, чем в нём уже есть. Как собрать в одном ведре 12 литров воды?
Задача 3.
Пять команд планируют провести однокруговой турнир матбоёв так, чтобы каждая команда играла не более одного боя в день и не более двух боёв в течение любых трёх дней подряд. За какое наименьшее число дней можно провести турнир?
Задача 4.
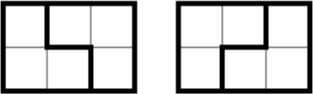
Прямоугольник 2 × 3 можно разрезать на трёхклеточные уголки двумя способами (см. рисунок). А существует ли клетчатая фигура, которую можно разрезать на такие уголки нечётным числом способов, большим одного?
Задача 5.
На прямой отмечена одна красная точка и шесть синих. Расстояние между каждыми двумя отмеченными точками равно целому числу сантиметров. При этом сумма расстояний от красной точки до синих равна 14 см. Найдите наибольшее возможное расстояние между двумя синими точками.
Задача 6.
На доске написано натуральное число. Оказалось, что между некоторыми его цифрами можно поставить знаки умножения (хотя бы один) так, что значение полученного выражения будет равно 2022. Какое наименьшее число может быть написано на доске?
Задача 7.
За круглым столом сидят трое: рыцарь, который всегда говорит правду, лжец, который всегда врёт, и дипломат, который иногда говорит правду, а иногда врёт. Сидящие за столом знают друг про друга, кто есть кто. Можно ли при помощи одного вопроса, требующего ответа «Да» или «Нет» и заданного одновременно всем троим, узнать, кто из них дипломат?
Задача 8.
У Матвея есть много кубиков 1 × 1 × 1. У каждого такого кубика на одной паре противоположных граней стоит по одной точке, на другой паре противоположных граней — по две точки, и на оставшейся паре противоположных граней — по три точки. Из восьми таких кубиков Матвей хочет сложить куб 2 × 2 × 2 так, чтобы количества точек на гранях этого куба были шестью последовательными натуральными числами. Удастся ли ему это?

