Гоша загадал число, а потом умножил его на произведение цифр этого числа. В результате вычислений у Гоши получилось 1197. Какое число мог загадать Гоша?

На плоскости нарисовано 12 равных отрезков и отмечены все точки их пересечения. Оказалось, что каждая точка пересечения делит каждый проходящий через неё отрезок в отношении 2 : 3. Какое наибольшее количество отмеченных точек может быть?

В каждой клетке доски 2022 × 2023 лежит монета. У монеты две стороны: орёл и решка. Разрешено выбрать строку или столбец и все монеты в этом ряду перевернуть. Также разрешено выбрать строку или столбец, подвинуть все монеты в этом ряду на одну клетку и выскочившую монету, не переворачивая, положить на освободившееся место с другой стороны доски. Можно ли, используя только эти две операции, добиться того, чтобы все монеты на доске лежали орлами вверх вне зависимости от того, как монеты лежали вначале?

Чип и Дейл едят орехи (запас орехов неограничен). Чип съел один орех, Дейл — два, Чип — три, Дейл — четыре и так далее. В итоге Чип съел 900 орехов. Сколько орехов мог съесть Дейл?

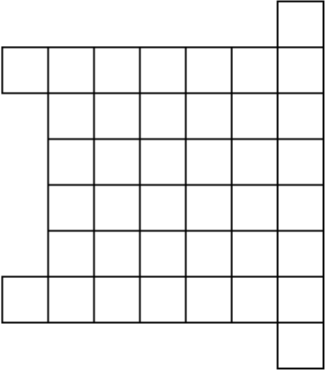
Клетчатую фигуру (см. рисунок) разбивают на двухклеточные доминошки. Вова посчитал число способов, где вертикальных доминошек больше, чем горизонтальных, а Гриша — где горизонтальных больше, чем вертикальных. Докажите, что они получили равные числа.

На доске написано шесть различных натуральных чисел. Никита записал в тетрадь одно из этих чисел, сумму каких-то двух записанных на доске чисел, сумму каких-то трёх записанных на доске чисел, . . . , сумму всех записанных на доске чисел. В итоге всего он записал шесть чисел. Какое наибольшее количество из них могли оказаться последовательными числами?

Великан Грохх положил в каждую клетку прямоугольника 3 × 4 булыжник. Веса булыжников попарно различны. Гермиона может указать на любую строку или любой столбец в прямоугольнике по своему усмотрению, а Грохх в ответ честно укажет на самый тяжёлый булыжник в этой строке или столбце соответственно. Сможет ли Гермиона с помощью таких операций гарантированно найти булыжник, который является одним из пяти самых тяжёлых?

На тротуаре выписаны в ряд 999 натуральных чисел, не обязательно различных и не обязательно упорядоченных по возрастанию или по убыванию. Петя обвёл красным мелком 500 чисел. Оказалось, что эти числа – 1, 2, . . . , 500, встречающиеся в ряду в порядке возрастания слева направо. Вася обвёл зелёным мелком 500 чисел. Оказалось, что эти числа – 500, 499, . . . , 1, встречающиеся в ряду в порядке убывания слева направо. Докажите, что центральное (то есть пятисотое) число ряда обведено дважды.