Задача 1.
Остаток от деления натурального числа на 2022 на 1000 больше, чем остаток от деления этого же числа на 2021. Найдите наименьшее такое число.
Задача 2.
Два двузначных числа таковы, что, если поменять местами цифры в каждом из них, сумма двух получившихся чисел будет вчетверо больше. Найдите все такие пары чисел.
Задача 3.
Министерство охраны секретов использует на своих объектах четырёхзначные коды (от 0000 до 9999). Чтобы запудрить мозги сотрудникам, оно хочет сопоставить каждому коду некоторый цвет. При этом, если у одного кода в каждом разряде стоит не меньшая цифра, чем у другого, цвета этих двух кодов не должны совпадать. Какое наименьшее количество цветов сможет использовать министерство?
Задача 4.
На острове есть два племени: лжецы, которые всегда лгут, и рыцари, которые всегда говорят правду. Каждый житель острова дружит со всеми соплеменниками и с некоторыми другими аборигенами. Каждый житель острова сказал, что среди его друзей соплеменники составляют большую часть. Докажите, что племя рыцарей многочисленнее.
Задача 5.
Петя одичал за время локдауна и теперь играет в странные игры с числами. Он начал писать в строчку бесконечную последовательность чисел, в начале которой стоят числа 0, 1 и −1. Во второй строке он пишет ту же последовательность со сдвигом на одну позицию вправо, а в третьей – ту же последовательность, сдвинутую ещё на одну позицию вправо. Там, где получились столбики из трёх чисел, он нашёл суммы чисел в столбиках, и оказалось, что эти суммы суть все кратные 3 в порядке возрастания. Вот как выглядит начало Петиной таблицы:
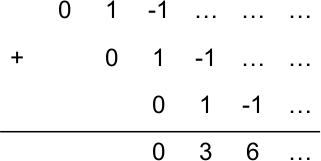
Какое число стоит в первой строке на 2022-м месте?
Задача 6.
Петя и Вася играют в игру на изначально пустой доске, делая ходы по очереди. Начинает Петя. За ход каждый игрок должен записать на доску натуральное число, которое до этого на доске ещё не встречалось. После того как каждый из игроков сделает по три хода, на доске окажется шесть натуральных чисел. Вася стремится к тому, чтобы эти шесть чисел можно было разбить на две группы по три числа таким образом, чтобы суммы чисел в группах были равны между собой. Сможет ли Петя помешать Васе осуществить свой план?
Задача 7.
Из клетчатого прямоугольника можно вырезать по клеткам 2022 фигурки вида (которые можно было поворачивать и переворачивать). Докажите, что из него можно вырезать по клеткам 2500 полосок 1 × 4.
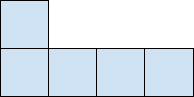
Задача 8.
На доске было написано натуральное число. Петя каждую минуту либо уменьшал число на какую-то его цифру, либо увеличивал (возможно, на цифру 0) — то есть сначала прибавил к числу его цифру, потом отнял от нового числа его цифру, потом снова прибавил и т.д. Через какое-то время на доске оказалось число 2022. Какое наименьшее число могло быть на доске в начале?

