Задача 1.
Бин и Бом решили развлечься. Бин выкладывает карточки с числами от 1 до 100 в некотором порядке, а Бом затем пытается переложить их по возрастанию. Бому разрешается поменять либо две карточки, лежащие через одну, либо две карточки, лежащие через четыре. Всегда ли Бому удастся это сделать?
Задача 2.
В классе 24 девочки и 25 мальчиков. На 23 февраля каждая девочка послала несколько смс-сообщений мальчикам с поздравлением, при этом каждая девочка поздравила менее половины мальчиков, но все девочки послали одно и то же количество сообщений. Докажите, что найдутся 2 мальчика, которые получили одно и то же количество поздравлений.
Задача 3.
На остановке стояли 30 рыцарей и лжецов. (Рыцари всегда говорят правду, а лжецы всегда врут.) Им задали вопрос: «Кого среди вас больше: рыцарей или лжецов?». «Больше лжецов» — ответили 8 человек, «Больше рыцарей» — ответили 12 человек, «Поровну» — ответили 10 человек. Сколько лжецов среди стоящих на остановке?
Задача 4.
Два брата Антонио и Борацио легли спать с твёрдым намерением собрать по утру яблок с 3-х яблонь их отца. Сначала проснулся Антонио и собрал половину всех яблок с одной из яблонь, треть всех яблок с другой из двух яблонь и шестую часть яблок с оставшейся яблони. Потом проснулся Борацио и собрал половину оставшихся яблок с какой-то из 3-х яблонь (не обязательно с той, с которой собрал половину Антонио), затем треть оставшихся яблок с другой из двух оставшихся яблонь и шестую часть с оставшейся яблони. Могли ли Антонио и Борацио собрать поровну яблок?
Задача 5.
Костя готовит лимонад на продажу. Для производства одной порции лимонада по Костиному рецепту требуется один лимон и полстакана сахара, оставшуюся часть составляет вода. Лимоны и сахар Костя покупает, а воду бесплатно набирает из-под крана. Стоимость одной порции состоит из стоимости затраченного на неё лимона, стоимости затраченного сахара, и оплаты Костиного труда. Костя продавал порцию лимонада за 10 рублей. Но однажды сахар подорожал в 3 раза. Из-за этого стоимость порции напитка возросла до 17 рублей. Потом лимоны подорожали в 3 раза. Из-за этого стоимость порции возросла до 25 рублей. Сколько денег с продажи каждой порции получает Костя за свой труд?
Задача 6.
Можно ли на прямой поставить 5 точек так, чтобы расстояние между какими-то двумя из них было 1 см, между какими-то двумя — 2 см, между какими-то двумя — 3 см, . . . , между какими-то двумя — 10 см?
Задача 7.
На столе лежат 5 одинаковых на вид золотых монет: две по 100 грамм, две по 99 грамм и одна 97 грамм. Как при помощи двухчашечных весов без стрелок за 2 взвешивания найти самую лёгкую монету?
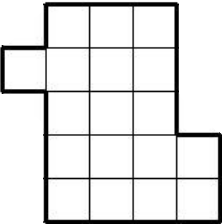
Задача 8.
Разрежьте фигуру, изображённую на рисунке, на две равные части (то есть одинаковые по форме и площади; части могут быть перевернутыми). Резать можно только по линиям сетки.