Задача 1.
Расшифруйте пример на умножение (т.е. вместо звёздочек нужно поставить цифры, возможно одинаковые, так, чтобы получилось верное равенство).
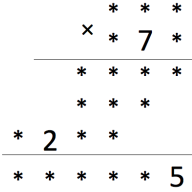
Задача 2.
Можно ли числа от 1 до 10 разбить на пять пар так, чтобы разности чисел в парах были равны 1, 2, 3, 4, 5?
Задача 3.
Имеется 26 шариков, каждый из которых красный, синий, жёлтый или зелёный, при этом в наборе есть хотя бы 1 шарик каждого цвета. Известно, что Антонио может разложить все эти шарики на 3 кучки так, что в каждой кучке синих шариков будет больше, чем красных. Борисио может разложить все эти шары на 4 кучки так, что в каждой кучке жёлтых будет больше, чем синих. Докажите, что их друг Вованио не сможет разложить все эти шары на 6 кучек так, что в каждой зелёных будет больше, чем жёлтых?
Задача 4.
Костя и Никита собирались за час (с 12:00 до 13:00) очистить футбольное поле от снега к приезду гостей. К сожалению, Никита проспал и опоздал к началу на 40 минут, в связи с этим к 13:00 поле было очищено лишь наполовину. Кто очищает поле от снега быстрее, Костя или Никита, и во сколько раз?
Задача 5.
Нарисуйте связную клетчатую фигуру, состоящую как минимум из 4 клеток, обладающую интересным свойством: если из этой фигуры вырезать любую клетку, то оставшуюся часть фигуры можно по линиям сетки разрезать на две одинаковые клетчатые фигуры.
Задача 6.
Турист на острове Рыцарей и Лжецов встретил четырёх аборигенов. «Кто ваши попутчики?» — спросил он у каждого из них. «Три лжеца», — ответили первые двое. «Рыцарь и два лжеца», — ответил третий. А что мог ответить четвёртый? (На острове живут рыцари, которые всегда говорят только правду, и лжецы, которые всегда лгут.)
Задача 7.
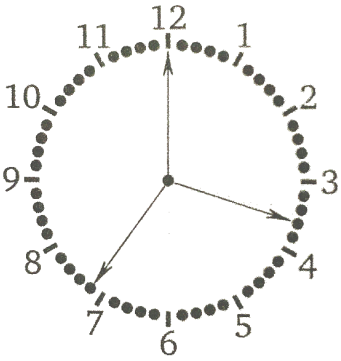
На циферблате механических часов секундная, минутная и часовая стрелка имеют одинаковую длину. Посмотрите на часы (см. рисунок) и скажите точное время. Не забудьте, конечно, объяснить, что вы нашли все возможные варианты ответа.
Задача 8.
Петя и Вася по очереди закрашивают один из треугольничков на поле (см. рисунок). Начинает Петя. Нельзя закрашивать треугольничек, если его сосед по стороне уже закрашен. Кто не может сделать ход — проиграл. Кто из ребят может выиграть в эту игру вне зависимости от игры соперника?


