Задача 1.
Решите ребус: Т + У = Р + Н + И = Р + М + Ё = Б ⋅ И = У + С ⋅ A. (Одинаковыми буквами заменены одинаковые цифры, разными — разные.)
Задача 2.
Существует ли 6-значное число, в котором нет одинаковых цифр и каждая цифра, начиная с третьей, равна сумме или разности двух предыдущих цифр? Нумерация цифр начинается со старшего разряда, т.е. слева направо.
Задача 3.
Петя и Вася играют в игру, начинает Петя. За один ход разрешается вырезать из доски 8 × 8 по линиям сетки одну из следующих фигур: квадратик 1 × 1, прямоугольник 1 × 2 или 2×1, уголок из 3 клеток; ходы делаются по очереди. Тот, кто не может сделать очередной ход, проигрывает. Кто выигрывает при правильной игре обоих игроков?
Задача 4.
Кран наполняет тазик водой. Сейчас кран открыт, тазик полон; котята начинают жадно пить воду из тазика. Известно, что 6 котят опустошат тазик за 5 минут, а 10 котят — за минуту. Какое количество котят смогут бесконечно утолять жажду из тазика при открытом кране?
Задача 5.
На столе лежат 4 пронумерованных алмаза, среди них 2 настоящих и 2 фальшивых. Пригласили эксперта, который может отличить настоящий алмаз от фальшивого. Вы можете показать эксперту любые 3 алмаза, он по своему усмотрению указывает на два из них и говорит, сколько среди выбранных алмазов настоящих – два, один или ни одного. Эту операцию можно повторять любое число раз. Покажите, как должен действовать эксперт, чтобы вы при всем желании не смогли определить ни одного настоящего алмаза или фальшивого алмаза.
Задача 6.
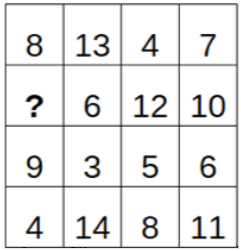
В таблице записаны числа. Одно из них, помеченное знаком вопроса, вы не видите, а Машенька и Наташенька видят. Машенька выбрала самое маленькое число в каждой строке и сложила их, Наташенька выбрала самое маленькое число в каждом столбце и тоже сложила эти числа. Сумма у Наташеньки получилась на 1 больше, чем у Машеньки. Какое число закрыто знаком вопроса?
Задача 7.
В клубе сидели 10 детей. Первый сказал: «В клубе больше 1 мальчика». Второй: «В клубе больше 2 мальчиков». И так далее. Пятый сказал: «В клубе больше 5 мальчиков». После этого шестой заметил: «В классе больше 1 девочки». Седьмой: «В классе больше 2 девочек». И так далее. Десятый заявил: «В классе больше 5 девочек». Известно, что девочки сказали правду, а мальчики соврали. Сколько в клубе может быть девочек?
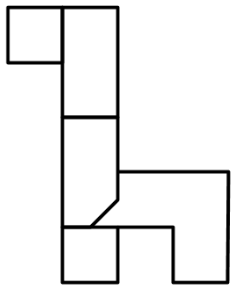
Задача 8.
Фигура альпака разделена на 5 частей (см. рисунок). Сколькими способами можно раскрасить фигуру в 3 цвета так, чтобы части одного цвета не имели общих точек? Каждая часть покрашена в один из 3 цветов.