Задача 1.
Длина взрослого червяка 1 метр, а червяки меньшей длины — молодые, червяков длиной более 1 метра не бывает. Если червяк взрослый, его можно разрезать на две части в любом отношении длин. При этом получаются два новых молодых червяка, которые сразу начинают расти со скоростью 1 метр в час каждый. Когда длина червяка достигает метра, он становится взрослым и прекращает расти. Как из одного взрослого червяка получить 3 взрослых червяка быстрее чем за 1 час?
Задача 2.
Белоснежка и 7 гномов несли яблоки в подарок Королеве. Белоснежка, считая яблоки, забыла посчитать свои, но дважды сосчитала яблоки гнома Простачка, в результате получила 23 штуки. Гном Простачок, считая яблоки, забыл сосчитать свои, но дважды посчитал Белоснежкины, в итоге получил 31. Сколько всего яблок несли Белоснежка и гномы?
Задача 3.
Можно ли выписать в строчку 26 трёхзначных чисел так, чтобы каждое следующее число в строчке было меньше предыдущего, но имело бóльшую чем у него сумму цифр?
Задача 4.
В первую минуту суток на электронных часах горит 00:00, а в последнюю — 23:59. Сколько времени в течение суток на часах не горит ни одна двойка?
Задача 5.
Вованио по нечётным числам любого месяца всегда говорит только правду, а по чётным обязательно лжёт. Вчера он сказал: «Завтра вторник», а на сегодня он заявил: «Вчера был понедельник». Какое число будет завтра?
Задача 6.
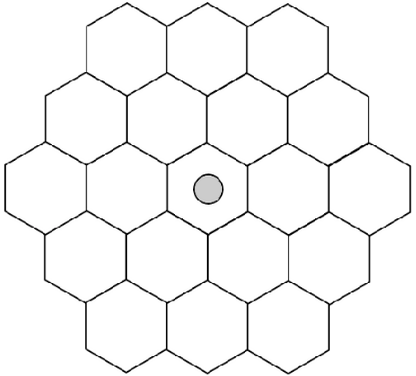
Поле разделено на 19 шестиугольников, в центральном шестиугольнике стоит фишка (см. рисунок). Двое по очереди делают ходы: за свой ход нужно передвинуть фишку в соседний по стороне шестиугольник, при этом запрещается ставить фишку в шестиугольник, в котором она уже была. Исходный центральный шестиугольник считается уже посещённым. Проигрывает тот, кто не может сделать очередной ход. Кто из игроков может обеспечить себе победу вне зависимости от действий другого игрока?
Задача 7.
Среди 8 одинаково выглядящих монет — четыре латунных и четыре медных. За одну пробу специальным тестером можно выяснить, сколько из монет в этой пробе латунных. (В пробу можно взять любое количество монет.) Требуется за две пробы найти пару разных монет — одну латунную и одну медную. Какая именно монета латунная, выяснять не требуется.
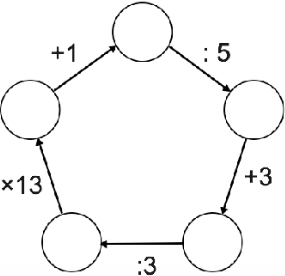
Задача 8.
Можно ли в каждый кружок вписать целое число так, чтобы все указанные на стрелках арифметические действия были верными?