Задача 1.
По кругу стоят 7 жителей острова Рыцарей и Лжецов. Один из них сказал «Среди нас есть рыцарь», другой: «Среди нас есть лжец», третий: «Среди нас есть два рыцаря, стоящих рядом», четвёртый: «Среди нас есть два лжеца, стоящих рядом», пятый: «Среди нас есть три рыцаря, стоящих подряд», шестой: «Среди нас есть три лжеца, стоящих подряд» и седьмой: «Среди нас есть рыцарь и лжец, стоящие рядом». Сколько лжецов может быть среди них? (Жителями острова Рыцарей и Лжецов являются рыцари, которые всегда говорят правду, и лжецы, которые всегда врут. Порядок, в котором они говорят, не обязательно совпадает с порядком, в котором они стоят по кругу.)
Задача 2.
Петя и Вася по очереди закрашивают один из треугольничков на поле (см. рисунок). Начинает Петя. Нельзя закрашивать треугольничек, если его сосед по стороне уже закрашен. Кто не может сделать ход — проиграл. Кто из ребят может выиграть в эту игру вне зависимости от игры соперника?

Задача 3.
Среди 6 одинаково выглядящих монет — две весящих по 10 г, две 12-граммовые и две по 13 г. Имеются весы со стрелкой, позволяющие узнать вес положенных на них монет. Как за два взвешивания разделить все монеты на две равных по весу кучки?
Задача 4.
4 велосипедиста участвовали в гонке-преследовании. Первым со старта уехал Антон, за ним Борис, потом Вова, последним начал гонку Гоша. После окончания гонки каждому из них задали вопрос: «Сколько обгонов с вашим участием было на протяжении гонки, то есть сколько раз вас обгоняли или вы кого-то обгоняли?»
- Антон ответил: «То ли 7, то ли 3 обгона».
- Боря: «Таких обгонов было 11 или 7».
- Вова: «19 или 20 обгонов».
- Гоша сказал: «Я не помню точное количество, но оно определенно больше 36».
Известно, что в течение гонки не было момента, когда три и более участников находились в одной точке. Сколько всего обгонов было на протяжении гонки?
Задача 5.
Имеется 26 шариков, каждый из которых красный, синий, жёлтый или зелёный, при этом в наборе есть хотя бы 1 шарик каждого цвета. Известно, что Антонио может разложить все эти шарики на 3 кучки так, что в каждой кучке синих шариков будет больше, чем красных. Борисио может разложить все эти шары на 4 кучки так, что в каждой кучке жёлтых будет больше, чем синих. Докажите, что их друг Вованио не сможет разложить все эти шары на 6 кучек так, что в каждой зелёных будет больше, чем жёлтых?
Задача 6.
Расшифруйте пример на умножение (т.е. вместо звёздочек нужно поставить цифры, возможно одинаковые, так, чтобы получилось верное равенство).
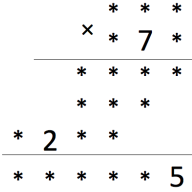
Задача 7.
Коля выписал на одну доску все числа от 1 до 100 в ряд в некотором порядке. Маша выписала на вторую доску все возможные суммы трёх подряд идущих чисел из ряда Коли (то есть Маша выписала всего 98 чисел). Какое наибольшее количество чисел, выписанных Машей, могут быть нечётными?
Задача 8.
Придумайте клетчатую фигуру, не являющуюся прямоугольником, такую, что из неё можно удалить две клетки, и она распадётся на две одинаковые части (которые не являются прямоугольниками), а можно удалить три клетки и она распадётся на четыре одинаковые части (которые так же не являются прямоугольниками).

