Задача 1.
25 рыцарей и лжецов пять дней собирались в клубе, при этом они каждый раз рассаживались за пять столов по пять человек (в разные дни они могли садиться по разному). В понедельник за каждым из столов один из сидящих сказал: «За моим столом сидит ровно один лжец». Во вторник за каждым из столов один из сидящих сказал: «За моим столом сидит ровно два лжеца». И так далее. В пятницу за каждым из столов один из сидящих сказал: «За моим столом сидит ровно пять лжецов». Оказалось, что в течении этих пяти дней каждый хотя бы раз произнёс какую-то фразу. Какое наименьшее количество лжецов могло быть среди них?
Задача 2.
Бабушка плохо различает цифры 5 и 6 (то есть 5 она может понять как 5, так и 6, то же самое с 6). У внука в тетради она увидела три числа: 605, 556, 6056. Могла ли сумма трёх чисел оказаться палиндромом, если бабушка увидела ровно 4 цифры неправильно?
Задача 3.
В футбольном чемпионате играют 18 команд. Каждая должна сыграть с каждой по одному разу, причём в каждом туре играют все команды, и все матчи тура проходят одновременно. Можно ли составить расписание чемпионата так, чтобы у каждой команды игры на своём поле и на выезде чередовались?
Задача 4.
Какое наибольшее количество фигурок можно вырезать из треугольника (см. рисунок)? Фигурки можно поворачивать и переворачивать.
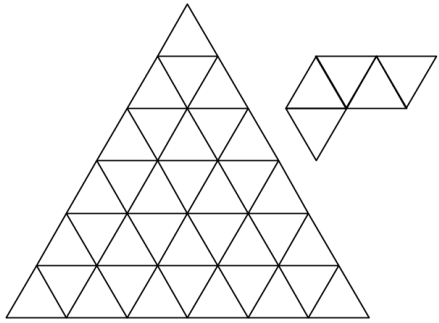
Задача 5.
Можно ли прямоугольник 4 × 6 клеток разрезать на три клетчатые фигуры так, чтобы фигура, у которой площадь самая большая, имела периметр самый маленький, а фигура, у которой площадь самая маленькая, имела периметр самый большой? (У всех фигур площади и периметры должны быть разными!)
Задача 6.
Мурзилка вышел из пункта 𝐴 в пункт 𝐵. Пройдя треть пути, он встретил почтальона Печкина, вышедшего ему навстречу из пункта 𝐵 10 минут назад. Когда Печкин пришёл в пункт 𝐴, Мурзилке осталось идти до 𝐵 в 4 раза больше времени, чем он шёл до момента выхода Печкина из 𝐵. Сколько времени Мурзилка шёл от 𝐴 до 𝐵?
Задача 7.
На складе имеется 120 кг сахара-песка. Покупатель хочет купить ровно 35 кг, но у кладовщика есть только одна 8-килограммовая гиря, двухчашечные весы и запас мешков. Помогите ему взвесить нужное количество, обойдясь всего трёмя взвешиваниями.
Задача 8.
На турнир матбоёв приехали Андрей, Борис, Вова, Гена и Дима. На второй бой они пришли в разных футболках этого турнира, на которых были написаны числа 1, 2, 3, 4, 5 (номера этого турнира), встали в ряд и по очереди сказали:
- — Число на Вовиной футболки чётное — сказал мальчик в футболке с 1-го турнира.
- — Произведение чисел на футболках Гены и Димы оканчивается на 0 — сказал Вова.
- — Сумма чисел на футболках моих соседей — чётное число, — сказал Гена.
- — Число на футболке Димы — самое большое, — сказал мальчик в футболке со 2-го турнира.
- — Число на моей футболке равно среднему арифметическому 1 и числа на футболке Вовы — сказал Дима.
Известно, что правду сказал только один мальчик. Какое число написано у него на футболке?

