Задача 1.
Число 7 обладает забавным свойством: если его умножить на 3, то сумма цифр уменьшится более чем вдвое (сумма цифр числа 21 равна 3, и 7/3 > 2). А существует ли такое натуральное число, что если его умножить на 3, то сумма цифр уменьшится более чем в 6 раз?
Задача 2.
Никита вырезал из листка бумаги многоугольник произвольной формы, а Костя одним взмахом ножниц разрезал его на треугольник и четырёхугольник. Сколько сторон мог иметь исходный многоугольник? Укажите все возможности.
Задача 3.
На столе лежат 2020 монет. Петя, Витя и Толя по очереди берут монеты со стола. Пете разрешается брать только одну монету, Вите – 1, 3, 5 или 7 монет, а Толе – 2, 4, 6 или 8. Если на столе остаётся всего одна монета, то Толя свой ход пропускает. Выигрывает тот, кто своим ходом сможет забрать последнюю монету. Кто выиграет при правильной игре, если Петя определяет порядок, в котором игроки будут делать ходы?
Задача 4.
Пузатостью прямоугольника назовём отношение его большей стороны к меньшей. Докажите, что можно разрезать квадрат площади 100 на четыре прямоугольника площади 10, 20, 30 и 40 так, чтоб пузатость каждого была меньше двух.
Задача 5.
В ряд стоят 10 жителей острова Рыцарей и Лжецов. Пятеро из них сказали: «Справа от меня в ряду есть рыцарь», а пятеро других сказали: «Слева от меня в ряду есть лжец». Какое наибольшее количество лжецов может быть среди них? (Жителями острова Рыцарей и Лжецов являются рыцари, которые всегда говорят правду, и лжецы, которые всегда врут)
Задача 6.
Найдите 2020-е по счёту натуральное число, которое нельзя представить в виде произведения двух последовательных натуральных чисел.
Задача 7.
На вступительной олимпиаде команды решили в среднем 4 задачи, при этом команды 4 класса решили в среднем 3,6 задачи, а команды 5 класса — 4,2 задачи. Сколько всего было команд, если их меньше 30?
Задача 8.
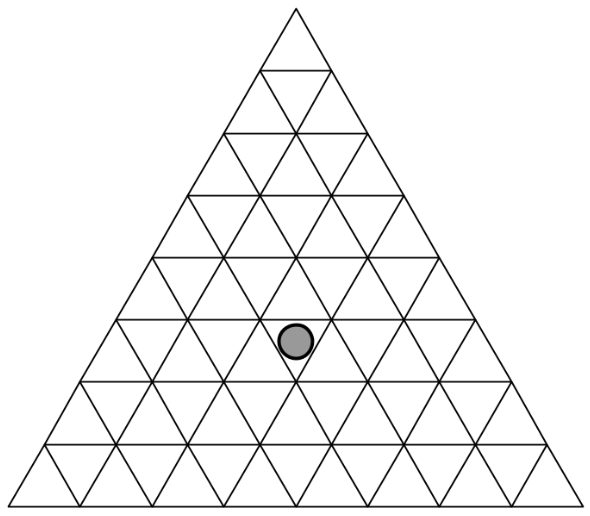
В центре треугольной доски стоит фишка (см. рисунок). Петя и Вася по очереди передвигают её в соседнее по стороне поле. Нельзя передвигать фишку в то поле, где она уже когда-то была (центральное поле считается посещённым). Проигрывает тот, кто не может сделать очередной ход. Кто может выиграть вне зависимости от игры соперника, если первым ходит Петя?