Задача 1.
Числовая операция ⊙ для любых двух положительных чисел 𝑎 и 𝑏 выполняется по такой формуле:
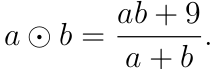
Чему равно значение выражения ((. . . (100 ⊙ 99) ⊙ 98) . . . ) ⊙ 2) ⊙ 1)?
Задача 2.
Вдоль окружности выписано несколько (больше 4) гласных и согласных букв. Серёжа обошел окружность по часовой стрелке и подсчитал, сколько раз встречаются фрагменты из четырёх рядом стоящих букв, в которых за гласной буквой идут три согласные, а Алина обошла окружность по часовой стрелке и подсчитала количество фрагментов, в которых за трёмя согласными следует гласная. У кого из них получился больший результат?
Задача 3.
На белой доске 8 × 8 чётное число клеток покрашены в чёрный цвет. За один ход Серёжа выбирает две соседние по стороне клетки и в обеих меняет цвет. Верно ли, что не более чем за 35 ходов он сможет покрасить в чёрный цвет всю доску?
Задача 4.
Постройте 12-угольник, все стороны которого лежат на шести прямых.
Задача 5.
Среди 6 одинаково выглядящих монет — две весящих по 10 г, две 12-граммовые и две по 13 г. Имеются весы со стрелкой, позволяющие узнать вес положенных на них монет. Как за два взвешивания разделить все монеты на две равных по весу кучки?
Задача 6.
Имеется 26 шариков, каждый из которых красный, синий, жёлтый или зелёный, при этом в наборе есть хотя бы 1 шарик каждого цвета. Известно, что Антонио может разложить все эти шарики на 3 кучки так, что в каждой кучке синих шариков будет больше, чем красных. Борисио может разложить все эти шары на 4 кучки так, что в каждой кучке жёлтых будет больше, чем синих. Докажите, что их друг Вованио не сможет разложить все эти шары на 6 кучек так, что в каждой зелёных будет больше, чем жёлтых?
Задача 7.
Расшифруйте пример на умножение (т.е. вместо звёздочек нужно поставить цифры, возможно одинаковые, так, чтобы получилось верное равенство).
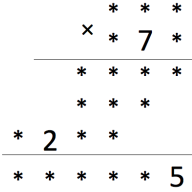
Задача 8.
Коля выписал на одну доску все числа от 1 до 100 в ряд в некотором порядке. Маша выписала на вторую доску все возможные суммы трёх подряд идущих чисел из ряда Коли (то есть Маша выписала всего 98 чисел). Какое наибольшее количество чисел, выписанных Машей, могут быть нечётными?

