Задача 1.
У Серёжи есть набор из 100 палочек, длины которых равны 2001, 2002, . . . , 2100. Каждая палочка покрашена в красный или синий цвет, причём сумма длин красных палочек равна сумме длин синих палочек. Серёжа хочет разрезать палочки так, чтобы их можно было разбить на пары, в каждой из которых одна красная и одна синяя палочка равной длины. Докажите, что для этого ему понадобится не менее 50 разрезов (каждую палочку можно резать несколько раз).
Задача 2.
Числовая операция ⊙ для любых двух положительных чисел 𝑎 и 𝑏 выполняется по такой формуле:
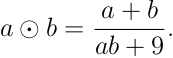
Чему равно значение выражения ((. . . (100 ⊙ 99) ⊙ 98) . . . ) ⊙ 2) ⊙ 1)?
Задача 3.
6-значное число 𝐴 приписали к самому себе, и оказалось, что получившееся число делится на 𝐴2. Чему могут быть равны первые две цифры числа 𝐴?
Задача 4.
Назовём раскраску клеток доски 8 × 8 в чёрный и белый цвета хорошей, если в ней чётное число чёрных клеток. За один ход Петя выбирает две соседние по стороне клетки и в обеих меняет цвет. Для каждой хорошей раскраски Серёжа посчитал, за какое наименьшее число ходов он сможет из этой раскраски получить раскраску, в которой все клетки чёрные. Чему равно самое большое из найденных Серёжей чисел?
Задача 5.
4 велосипедиста участвовали в гонке-преследовании. Первым со старта уехал Антон, за ним Борис, потом Вова, последним начал гонку Гоша. После окончания гонки каждому из них задали вопрос: «Сколько обгонов с вашим участием было на протяжении гонки, то есть сколько раз вас обгоняли или вы кого-то обгоняли?»
- Антон ответил: «То ли 7, то ли 3 обгона».
- Боря: «Таких обгонов было 11 или 7».
- Вова: «19 или 20 обгонов».
- Гоша сказал: «Я не помню точное количество, но оно определенно больше 36».
Известно, что в течение гонки не было момента, когда три и более участников находились в одной точке. Сколько всего обгонов было на протяжении гонки?
Задача 6.
Дан правильный восьмиугольник, его стороны задают 8 прямых. Какое наибольшее количество сторон может быть у многоугольника, все его вершины лежат на этих прямых и не совпадают с вершинами восьмиугольника?
Задача 7.
Среди 6 одинаково выглядящих монет — две весящих по 10 г, две 12-граммовые и две по 13 г. Имеются весы со стрелкой, позволяющие узнать вес положенных на них монет. Как за два взвешивания разделить все монеты на две равных по весу кучки?
Задача 8.
В треугольнике 𝐴𝐵𝐶 углы 𝐵 и 𝐶 равны 19º и 38º соответственно. 𝐴𝐷 ⊥ 𝐴𝐵, 𝐷 ∈ 𝐵𝐶. Докажите, что 𝐵𝐷 = 2𝐴𝐶.

