Задача 1.
На столе лежат сто пронумерованных алмазов, среди них 50 настоящих и 50 фальшивых. Пригласили эксперта, который может отличить настоящий алмаз от фальшивого. Эксперту показывают три алмаза, он указывает на два из них и говорит, сколько среди выбранных алмазов настоящих – два, один или ни одного. Определите, можно ли найти все настоящие алмазы вне зависимости от того, какие пары алмазов выбирает эксперт.
Задача 2.
Петя и Вася играют в игру на квадратном поле 8 × 8, начинает Петя. За один ход разрешается вырезать из доски по линиям сетки любой квадратик 1 × 1, в том числе из внутренней части доски; ходы делаются по очереди, пока каждый игрок не сделает по 2 хода. После этих 4 (двух парных) ходов на доске остаются 60 клеток. Если полученную в результате действий игроков фигуру можно разрезать по линиям сетки на две одинаковые части, то выигрывает Петя, в противном случае выигрывает Вася. Кто выигрывает при правильной игре обоих игроков?
Задача 3.
Докажите, что для любого количества нулей в числе 200.....01 существует такое кратное ему число, которое записывается только нечётными цифрами.
Задача 4.
Может ли сумма цифр натурального числа 𝑁 быть ровно вчетверо больше суммы цифр числа 2𝑁 ?
Задача 5.
Вася нарисовал на листе бумаги две одинаковых трёхзвенных ломаных и отметил все точки пересечения (в том числе отмечается и пересечение ломаной с ней самой). Какое наибольшее число точек у него могло получиться?
Задача 6.
Можно ли прямоугольник 2020 × 2021 разрезать на фигурки, изображённые ниже, так, чтобы «уголков» было в 4 раза больше, чем квадратиков 2 × 2 и в 2,5 раза меньше, чем «скобок»?
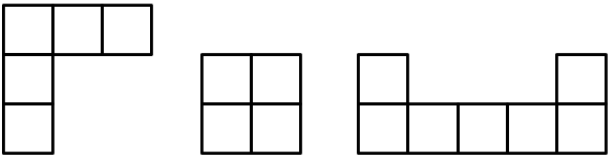
Задача 7.
На столе лежат 𝑁 карточек с числами от 1 до 𝑁. Костя и Никита взяли по 6 карточек. Оказалось, что произведения чисел на карточках у каждого из них одинаковы. При каком наименьшем 𝑁 это могло случиться?
Задача 8.
Каждая клетка доски 5 × 10 покрашена в чёрный или белый цвет. Каждая клетка граничит по стороне хотя бы с одной клеткой другого цвета. Докажите, что чёрных клеток хотя бы 10.

