Задача 1.
Для работы электрического фонарика нужны две исправных батарейки. У вас есть пять батареек, из которых исправны всего три, но вы не знаете, какие именно. Вы можете вставить в фонарик любую пару батареек, и если лампочка фонарика загорится, значит, обе батарейки рабочие. Назовём такую операцию одной пробой. Сумеете ли вы гарантированно найти 2 рабочие батарейки не более чем за 3 пробы? При этом эти батарейки не обязательно должны стоять в фонарике.
Задача 2.
Можно ли числа от 1 до 19 по одному расставить в треугольные клетки доски на рисунке ниже так, чтобы разница между любыми двумя числами в соседних по стороне треугольных клетках была не больше 2?
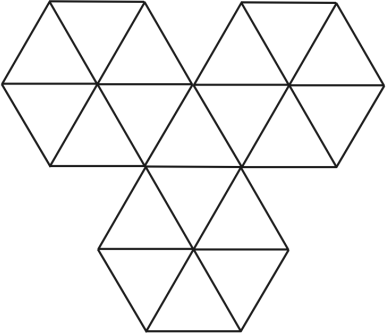
Задача 3.
Разрежьте фигуру на рисунке ниже, состоящую из 18 треугольников, на 2 одинаковые части по линиям сетки.
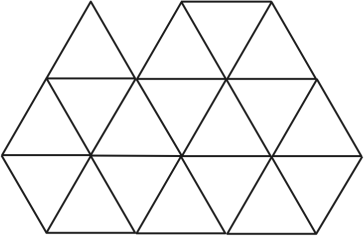
Задача 4.
Ауди, БМВ, Вольво ушли со старта гонок именно в таком порядке (А – 1, Б – 2, В – 3). Оказалось, что за время гонки Ауди обгоняли 3 раза, БМВ обгоняли 7 раз, а Вольво обгоняли 10 раз. В каком порядке могли финишировать машины?
Задача 5.
На встречу шпионов приехали 3 шпиона. Каждый приехал на автомобиле, либо мотоцикле (у автомобиля 4 колёса, у мотоцикла – 2).
- Фьюри: «Я приехал третьим».
- Томми: «Лэнс приехал вторым».
- Фьюри: «Перед моим приездом на парковке было 8 колёс».
- Томми: «Сейчас на парковке 12 колёс».
А Лэнс промолчал. Известно, что шпионы один раз сказали правду, другой солгали. Определите, в каком порядке шпионы приехали на встречу.
Задача 6.
Можно ли расставить в квадрате 4 × 4 короля, двух ладей и двух слонов так, чтобы ни одна из этих фигур не била никакую другую (все фигуры бьют по шахматным правилам).
Задача 7.
Известно, что 2021 год не является високосным. Никите на Новый год подарили отрывной календарь на 2021 год. В нём для каждого дня года был отдельный листочек. Никита оторвал столько листов с датами в этом календаре, что в календаре осталось в 4 раза больше листов с датами, чем оторвал Никита. Какая дата сейчас на календаре Никиты?
Задача 8.
На кружок танцев ходит 4 девочки и 3 мальчика. Учитель танцев должен выстроить всех семерых в ряд. Девочки ни за что не согласятся стоять на краю ряда. Сколькими способами учитель танцев сможет выстроить их в ряд, учитывая пожелания девочек?

