Натуральное число называется составным, если у него есть больше 2 натуральных делителей, считая само число и единицу. Например, число 6 — составное, так как у него 4 натуральных делителя: 1, 2, 3 и 6. Докажите, что любое натуральное число вида 66 . . . 64 (число шестёрок не равно 0) можно представить в виде суммы двух нечётных составных чисел.

В параллели пятых классов 71 ученик. 3/8 всех мальчиков и 5/11 всех девочек посещают различные кружки и факультативы. Сколько мальчиков в параллели?

Однажды Знайка сделал 2 заявления: «Вчера было такое число календаря, что в его записи встречалась цифра 9!» и «Завтра такое число календаря, что в его записи встретится цифра 2!» Сколько в календарном году может быть таких дней, когда Знайка окажется прав в обоих утверждениях?

Представим себе шахматную доску 3 × 4 (три столбца, четыре строки), в левом нижнем углу которой (на поле a1) стоит белый ферзь, а в правом верхнем (на поле c4) — чёрный король. Ферзь и король ходят по обычным правилам шахмат, первым ходит белый ферзь. Может ли ферзь добиться того, чтобы чёрный король оказался в правом нижнем углу доски (на поле c1)?

По дороге в школу Петя треть всего времени бежал вприпрыжку, треть — шёл шагом, а ещё треть — полз по-пластунски. Весь путь в школу у него занял 36 минут. Обратно из школы он только бежал вприпрыжку и шёл шагом. При этом вприпрыжку обратно он пробежал такое же расстояние, как и вприпрыжку по дороге в школу, а всё остальное расстояние прошёл пешком. Сколько времени заняла дорога домой, если Петя ползает по-пластунски в 2 раза медленнее, чем идёт шагом и втрое медленнее, чем бежит вприпрыжку?

Группа из 9 туристов оказалась ночью в тёмном-претёмном лесу у подножия горы с одним фонариком, работающим от 5 новых батареек ровно 3 часа. У группы туристов в рюкзаках оказалось 7 новых батареек. Смогут ли туристы так распорядиться фонариком и батарейками, чтобы фонарик в сумме проработал хотя бы 4 часа?

За круглым столом в каком-то порядке сидят 12 рыцарей и 12 лжецов. У каждого есть 2 карточки: красная и чёрная. Они по очереди передают своему соседу справа по одной карточке, причём рыцарь передаёт карточку того же цвета, что и получил, а лжец — другого цвета. Тот, кто передаёт карточку первым в круге, может выбрать для первого шага любую из своих карточек. Когда у всех впервые снова стало по две карточки (прошёл 1 круг), начинающего спросили: «Ваши карточки одинакового цвета?» Что он мог ответить?

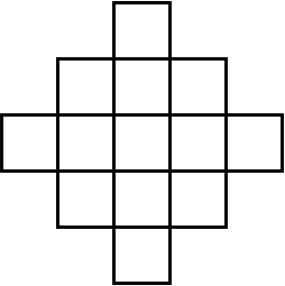
Миша записал в каждую из 13 клеток «крестика» на рисунке какое-то число. Оказалось, что сумма чисел в любом прямоугольнике 1 × 3 (расположенном вертикально или горизонтально) равна 18. Какое наибольшее количество попарно различных чисел могло быть записано в этот «крестик»?