Задача 1.
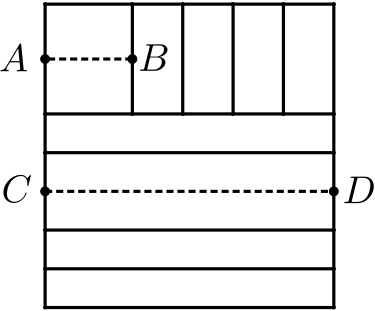
Коля разрезал квадрат на 11 прямоугольников так, как показано на рисунке. Оказалось, что площади всех 11 прямоугольников равны между собой. Длина отрезка 𝐴𝐵 = 19 см. Чему равна длина отрезка 𝐶𝐷?
Задача 2.
На острове Рыцарей и Лжецов турист повстречал трёх аборигенов. Абориген 𝐴 сказал туристу: «Ровно один из нас троих — лжец», после этого абориген 𝐵 заявил: «Все мы лжецы». В конце турист спросил у 𝐶: «Верно ли, что 𝐴 лжец?». Всегда ли по ответу аборигена 𝐶 турист сможет понять, из какого племени абориген 𝐴?
Задача 3.
Назовём натуральное число улиткой, если его запись состоит из записей трёх последовательных натуральных чисел, приписанных друг к другу в порядке возрастания: например, 8910 или 456 или 787980. Сколько существует натуральных пятизначных чисел, каждое из которых можно представить в виде суммы двух улиток?
Задача 4.
У ослика Иа-Иа есть 100 палочек. Длина каждой палочки – 3 см или 4 см. Докажите, что, разломав не более одной палочки, Иа-Иа сможет из всех палочек (теперь у него их 101, т.к. палочка ломается на две части) сложить прямоугольник.
Задача 5.
Барон Мюнхгаузен утверждает, что существует такое натуральное число, что если его последнюю цифру переставить в начало, то получится новое число, которое в 4 раза больше исходного. Не ошибается ли барон?
Задача 6.
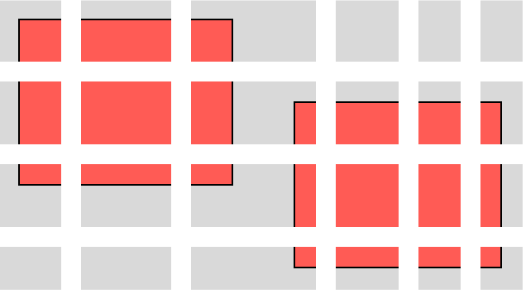
На красный прямоугольник положили сверху две горизонтальных и две вертикальных белых полоски шириной 1 м так, как показано на рисунке. При этом площадь, оставшаяся красной, равна 48 кв.м. После этого на точно такой же прямоугольник положили три вертикальных и две горизонтальных полоски ширины 1 м так, как показано на рисунке. Во второй раз красная площадь оказалась равна 40 кв.м. Найдите стороны исходного красного прямоугольника. Нужно найти, конечно, все возможные варианты. Стороны исходного прямоугольника могут быть нецелыми!
Задача 7.
Миллиардер Милон Аск прибыл на Марс и обнаружил там марсиан трёх видов. У марсианина может быть 1 голова и 2 ноги, либо 4 ноги и 3 головы, либо 7 голов и четыре пары ног. Милон насчитал у 300 вышедших его встречать марсиан 1000 ног. Сколько голов мог насчитать Милон у всех этих марсиан?
Задача 8.
У Никиты есть 4 внешне одинаковых монеты, которые весят 1, 2, 3 и 4 грамма соответственно. Никита не знает, где какие монеты. Никита сравнивает веса монет на чашечных весах (на каждую чашу вмещается всего 1 монета). Никита сделал 5 различных взвешиваний, после этого оказалось, что невозможно определить, какая из монет весит 4 грамма. Какую пару монет Никита точно ещё не взвешивал?

