Задача 1.
Семи из одиннадцати детей одной семьи задали вопрос: «Сколько у тебя сестёр?» Все семеро ответили: «У меня 8 сестёр». Сколько в семье сыновей?
Задача 2.
На доске в ряд написаны тридцать пятёрок. Антон поставил между некоторыми пятёрками знак «+». После этого оказалось, что полученная сумма равна 600. Сколько знаков «+» мог поставить Антон? Нужно указать, конечно, все возможные варианты и показать, что других вариантов нет!
Задача 3.
Света записала на картонной полосе цифры даты, которая будет ровно через год: 05042022. А потом разрезала полосу на 4 части так, что у неё получились 4 различных числа. Какая самая большая сумма этих четырёх чисел могла у неё получиться? (Числа не могут начинаться с цифры 0, кроме числа нуль.)
Задача 4.
Можно ли вписать в кружочки на рисунке числа от 1 до 7 каждое по одному разу так, чтобы суммы трёх чисел на всех шести линиях на рисунке были одинаковыми?
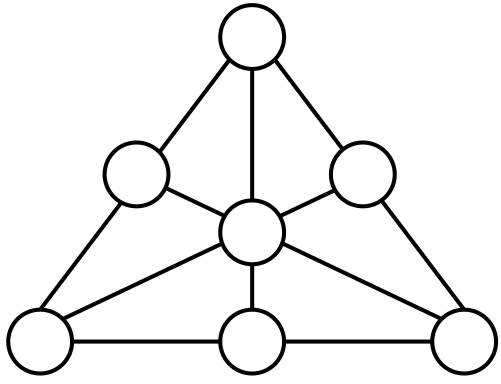
Задача 5.
У Кости есть 6 монет. Две из них весят по 20 г, две — по 21 грамм и две — по 22 грамма. Все монеты выглядят одинаково. Как за 3 взвешивания на чашечных весах без гирь найти две одинаковые по массе монеты?
Задача 6.
Из прямоугольника 6 × 7 вырезали доминошку 1 × 2 (см. рисунок). Разрежьте оставшуюся фигуру из 40 клеток на две одинаковые части по линиям сетки. Напоминаем, что фигуры называются одинаковыми, если их можно совместить наложением. Фигуры можно поворачивать и переворачивать.
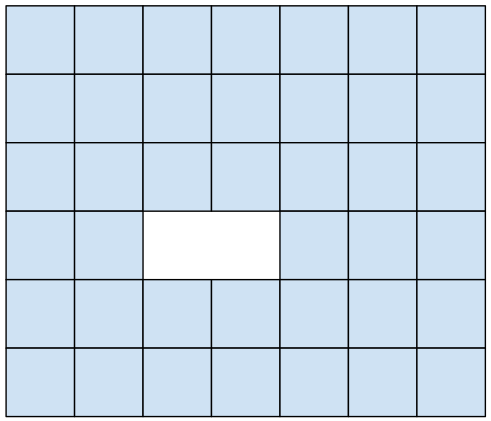
Задача 7.
В куче лежит 2022 камня. Антон, Боря и Вова по кругу (начинает Антон) берут из кучи от 1 до 4 камней каждый. Тот, кто не может сделать очередной ход, проигрывает. Докажите, что Боря и Вова могут сговориться и играть так, чтобы Антон проиграл.
Задача 8.
Из доски 101 × 101 по линиям сетки вырезано 101 прямоугольник 2 × 1 или 1 × 2 так, что вырезанные прямоугольники не имеют общих точек, и при этом никакой из вырезанных прямоугольников не примыкает к границе квадрата 101 × 101. Сколькими способами из оставшейся доски можно вырезать квадратик 2 × 2?

