Задача 1.
Для работы электрического фонарика нужны две исправных батарейки. У вас есть шесть батареек, из которых исправны всего три, но вы не знаете, какие именно. Вы можете вставить в фонарик любую пару батареек, и если лампочка фонарика загорится, значит, обе батарейки рабочие. Назовём такую операцию одной пробой. Сумеете ли вы гарантированно зажечь лампочку не более чем за 6 проб?
Задача 2.
Из прямоугольника 5 × 7 определённым образом (см. рисунок ниже) вырезали из одного угла доминошку 1 × 2, а из других углов вырезали по 1 клетке. Разрежьте оставшуюся фигуру из 30 клеток на две одинаковые части по линиям сетки. Фигуры называются одинаковыми, если их можно совместить наложением. Фигуры можно поворачивать и переворачивать.
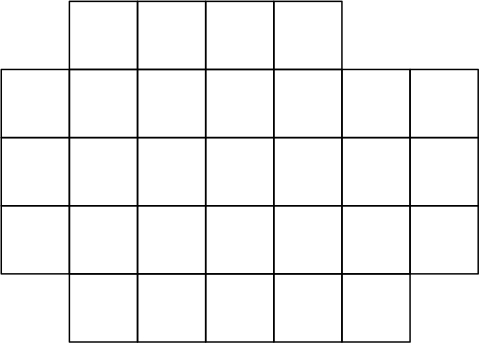
Задача 3.
Ауди, БМВ, Вольво и Жигули ушли со старта гонок именно в таком порядке (А – 1, Б – 2, В – 3, Ж – 4). Оказалось, что за время гонки Ауди обгоняли 1 раз, БМВ обгоняли 3 раза, Вольво обгоняли 5 раз, а Жигули обгоняли 9 раз. Кто мог финишировать первым?

