Задача 1.
Прямоугольник, периметр которого 1 метр, двумя вертикальными и трёмя горизонтальными разрезами разделили на 12 одинаковых меньших прямоугольников. Чему равна площадь исходного прямоугольника, если сумма длин всех разрезов равна 115 см?
Задача 2.
Назовём натуральное число «интересным», если все его цифры чётны. Назовём натуральное число «очень интересным», если оно «интересное» и для него не существует меньшего его «интересного» натурального числа с такой же суммой цифр. Митя записал на доску натуральное число, которое было «очень интересным», а его сумма цифр была равна 2022. Чему могла быть равна цифра самого старшего разряда в этом числе? Нужно найти все возможные варианты.
Задача 3.
Существуют ли два таких трёхзначных числа 𝐴 и 𝐵, что в числе 𝐴 все цифры различны и нечётны, а в числе 𝐵 все цифры различны и чётны, при этом число 𝐵 нацело делится на число 𝐴?
Задача 4.
В Динарии в ходу две валюты — динары и сольдо. Если заплатить за двух слонов 30 динаров, то на сдачу можно получить 2 сольдо. Если заплатить 20 динаров, то можно купить одного слона и получить 4 сольдо сдачи. Сколько динаров сдачи будет, если за слона заплатить 17 сольдо?
Задача 5.
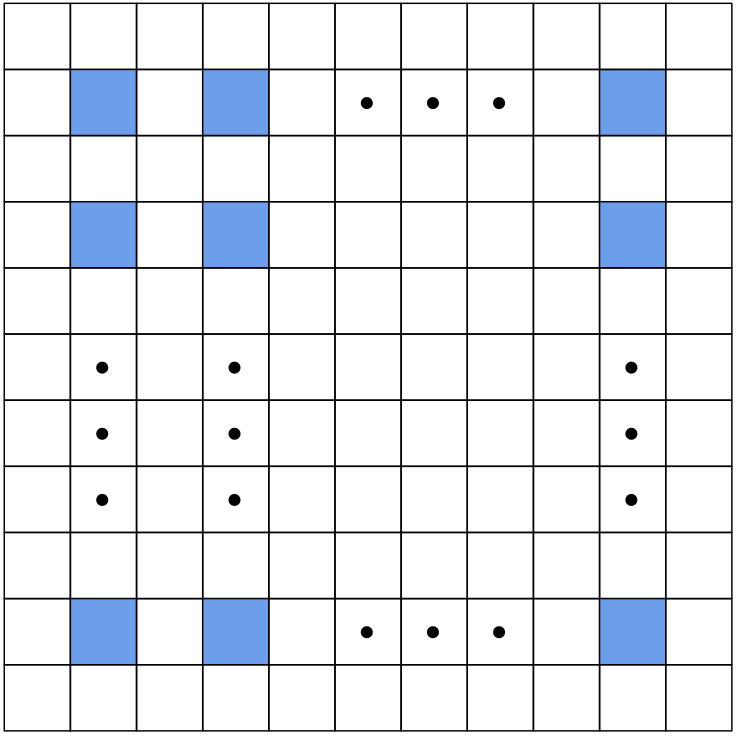
Из доски 2001 × 2001 клетки вырезаны в определённом порядке (см. рисунок, закрашенные клетки вырезаны). Сколькими способами из оставшейся доски можно вырезать по линиям сетки трёхклеточный уголок?
Задача 6.
На конференцию приехали математики, физики и программисты. Во время церемонии открытия некоторые участники пожали друг другу руки. Оказалось, что каждый математик пожал руку восьми физикам и двенадцати программистам. Каждый физик пожал руку четырём математикам и шести программистам. Каждый программист пожал руку трём физикам и 𝑛 математикам. Определите, чему равно 𝑛.
Задача 7.
Имеется белая полоска из 8 клеток. Вася и Петя по очереди закрашивают клетки. Начинает Петя. За один ход можно закрасить в чёрный цвет одну или две белые клетки (не обязательно стоящие рядом). Тот, после чьего хода не остаётся рядом стоящих белых клеток, — проигрывает. Кто выигрывает при правильной игре?
Задача 8.
Учитель называет подряд все трёхзначные числа, а Матвей для каждого названного числа записывает произведение его цифр. Сколько чисел будут записаны Матвеем ровно один раз?

