Задача 1.
Можно ли расставить в квадрате 4 × 4 короля, двух ладей и двух слонов так, чтобы ни одна из этих фигур не била никакую другую (все фигуры бьют по шахматным правилам).
Задача 2.
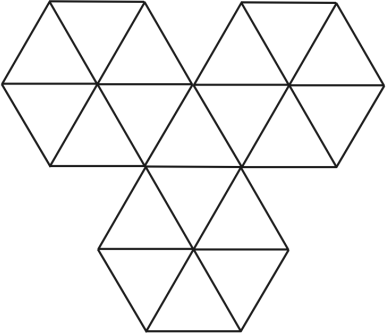
Можно ли числа от 1 до 19 по одному расставить в треугольные клетки доски на рисунке ниже так, чтобы разница между любыми двумя числами в соседних по стороне треугольных клетках была не больше 2?
Задача 3.
Сколькими способами можно расставить числа от 1 до 15 в ряд так, чтобы сумма любых двух соседних чисел была квадратом натурального числа?
Задача 4.
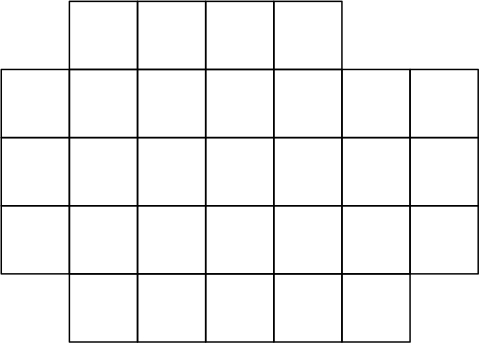
Из прямоугольника 5 × 7 определённым образом (см. рисунок ниже) вырезали из одного угла доминошку 1 × 2, а из других углов вырезали по 1 клетке. Разрежьте оставшуюся фигуру из 30 клеток на две одинаковые части по линиям сетки. Фигуры называются одинаковыми, если их можно совместить наложением. Фигуры можно поворачивать и переворачивать.
Задача 5.
Для работы электрического фонарика нужны две исправных батарейки. У вас есть восемь батареек, из которых исправны пять, но вы не знаете, какие именно. Вы можете вставить в фонарик любую пару батареек, и если лампочка фонарика загорится, значит, обе батарейки рабочие. Назовём такую операцию одной пробой. За какое наименьшее число проб вы гарантированно сумеете найти две рабочих батарейки.
Задача 6.
Семь пиратов делили награбленное – пять одинаковых сундуков с сокровищами. Они договорились, что пятеро из них возьмут себе по сундуку, а остальным выплатят справедливую компенсацию. Каждый из получателей сундука заплатил по 10000 пиастров. В какую сумму пираты оценили один сундук?
Задача 7.
В футболе победитель матча получает 3 очка, проигравший – 0, а каждая из команд, сыгравших вничью, получает по 1 очку. Команда «Зубило» сыграла в круговом турнире на 7 команд и набрала в нём 5 очков, при этом забила 4 гола, а пропустила 3. С каким счётом закончились все матчи команды «Зубило»?
Задача 8.
Прямоугольник, периметр которого 100 см, семью вертикальными и десятью горизонтальными разрезами разделили на 88 одинаковых меньших прямоугольников. Чему равен периметр каждого из них, если сумма длин всех разрезов равна 434 см?

