Задача 1.
На острове Рыцарей и Лжецов турист повстречал четырёх аборигенов 𝐴, 𝐵, 𝐶 и 𝐷. 𝐴 сказал туристу «Ровно один из нас четверых – лжец», а 𝐵 сказал «Все мы лжецы». Тогда турист спросил у 𝐶 «Верно ли, что 𝐴 лжец», и по ответу 𝐶 («Да» или «Нет») смог определить, является ли лжецом. Кто из них может быть лжецами?
Задача 2.
Каждый пятиклассник, поехавший в летний лагерь, занимается в одном или двух из трёх кружков – математическом, физическом или программистском. Тех, кто занимается только в маткружке, вдвое меньше, чем тех, кто занимается только в программистском кружке, и в целое число раз больше, чем занимающихся только в физическом. Кроме того, что ровно 1/10 среди посещающих маткружок — программисты, ровно 1/10 среди посещающих кружок по программированию — физики, и ровно 1/10 среди посещающих кружок по физике – математики. Какая часть всех детей занимается в двух кружках?
Задача 3.
Весы со стрелкой сломаны — при каждом взвешивании показывают либо на 1 г больше, чем истинный вес, либо на 1 г меньше. У Кости есть четыре монеты, три из которых настоящие, а одна фальшивая — весит больше или меньше настоящей. Сможет ли Костя отыскать фальшивую монету с помощью имеющихся весов? Число взвешиваний не ограничено.
Задача 4.
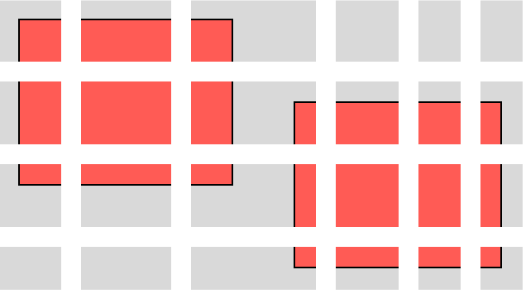
На красный прямоугольник положили сверху две горизонтальных и две вертикальных белых полоски шириной 1 м так, как показано на рисунке. При этом площадь, оставшаяся красной, равна 48 кв.м. После этого на точно такой же прямоугольник положили три вертикальных и две горизонтальных полоски ширины 1 м так, как показано на рисунке. Во второй раз красная площадь оказалась равна 40 кв.м. Найдите стороны исходного красного прямоугольника. Нужно найти, конечно, все возможные варианты. Стороны исходного прямоугольника могут быть нецелыми!
Задача 5.
Числа от 1 до 20 разбили на две [непустые] группы и в каждой группе сосчитали среднее арифметическое. Может ли сумма этих двух средних быть равна 12?

