Задача 1.
Имеется белая полоска из 100 клеток. Вася и Петя по очереди закрашивают клетки. Начинает Петя. За один ход можно закрасить в чёрный цвет одну или две белые клетки (не обязательно стоящие рядом). Тот, после чьего хода не остаётся рядом стоящих белых клеток, — проигрывает. Кто выигрывает при правильной игре?
Задача 2.
Учитель называет подряд все трёхзначные числа, а Матвей для каждого названного числа записывает произведение его цифр. Сколько чисел будут записаны Матвеем ровно один раз?
Задача 3.
Существуют ли два таких трёхзначных числа 𝐴 и 𝐵, что в числе 𝐴 все цифры различны и нечётны, а в числе 𝐵 все цифры различны и чётны, при этом число 𝐵 нацело делится на число 𝐴?
Задача 4.
В Динарии в ходу две валюты — динары и сольдо. Если заплатить за двух слонов 30 динаров, то на сдачу можно получить 2 сольдо. Если заплатить 20 динаров, то можно купить одного слона и получить 4 сольдо сдачи. Сколько динаров сдачи будет, если за слона заплатить 17 сольдо?
Задача 5.
На конференцию приехали математики, физики и программисты. Во время церемонии открытия некоторые участники пожали друг другу руки. Оказалось, что каждый математик пожал руку восьми физикам и двенадцати программистам. Каждый физик пожал руку четырём математикам и шести программистам. Каждый программист пожал руку трём физикам и 𝑛 математикам. Определите, чему равно 𝑛.
Задача 6.
Назовём натуральное число «интересным», если все его цифры чётны. Назовём интересное число «удивительным», если для него не существует меньшего его интересного числа с той же суммой цифр. Митя записал на доску удивительное число с суммой цифр 2022. Чему могла быть равна цифра в самом старшем разряде в этом числе? Нужно найти все возможные варианты.
Задача 7.
У трёх сестёр Веры, Надежды и Любови дни и месяцы рождения совпадают — 30 сентября. В день, когда старшей сестре Вере исполнилось 18 лет, сумма возрастов всех сестёр делилась на 18. Спустя несколько лет, в день 18-летия Надежды, эта ситуация повторилась. Сколько лет будет каждой сестре, когда младшей сестре (Любови) исполнится 18?
Задача 8.
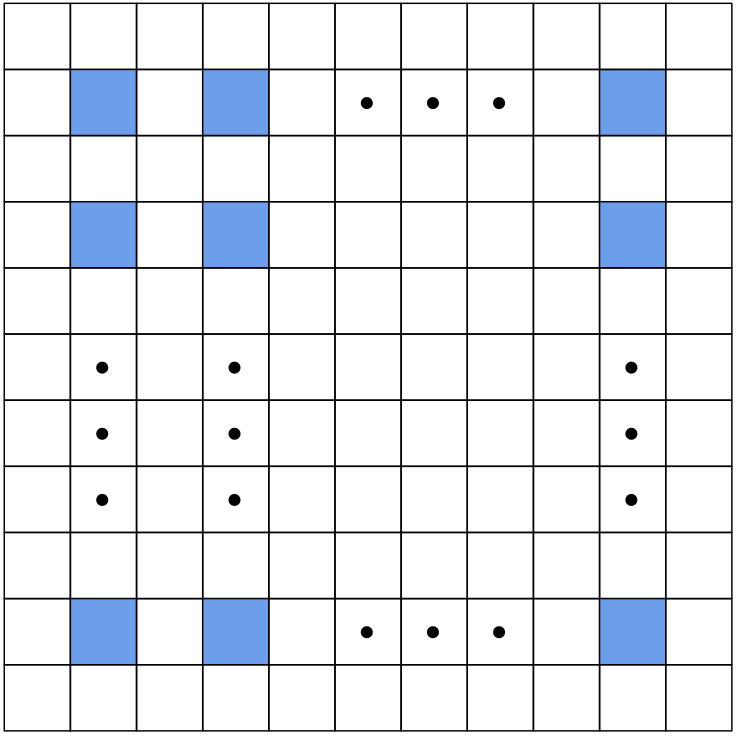
Из доски 2001 × 2001 клетки вырезаны в определённом порядке (см. рисунок, закрашенные клетки вырезаны). Сколькими способами из оставшейся доски можно вырезать по линиям сетки трёхклеточный уголок?