Задача 1.
У ослика Иа-Иа есть 100 палочек. Длина каждой палочки – 3 см или 4 см. Докажите, что, разломав не более одной палочки, Иа-Иа сможет из всех палочек (теперь у него их 101, т.к. палочка ломается на две части) сложить прямоугольник.
Задача 2.
Коля разрезал квадрат на 11 прямоугольников так, как показано на рисунке. Оказалось, что площади всех прямоугольников равны между собой. Во сколько раз длина отрезка 𝐴𝐵 меньше длины отрезка 𝐶𝐷?
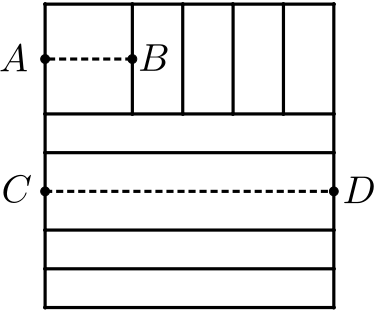
Задача 3.
На острове Рыцарей и Лжецов турист повстречал трёх аборигенов. Абориген 𝐴 сказал туристу: «Ровно один из нас троих — лжец», после этого абориген 𝐵 заявил: «Все мы лжецы». В конце турист спросил у 𝐶: «Верно ли, что 𝐴 лжец?». Всегда ли по ответу аборигена 𝐶 турист сможет понять, из какого племени абориген 𝐴?
Задача 4.
С помощью знаков арифметических действий + – × : , скобок, а также используя каждую из цифр 1, 5, 6, 7 ровно по одному разу, составьте выражение, значение которого равно 35.
Задача 5.
Света играет в дартс. К сожалению, она играет не очень хорошо, поэтому не может попасть дротиком в зону мишени, в которую уже попала, и во все соседние зоны. В каждой зоне отмечено количество баллов, которое получает игрок при попадании дротиком.
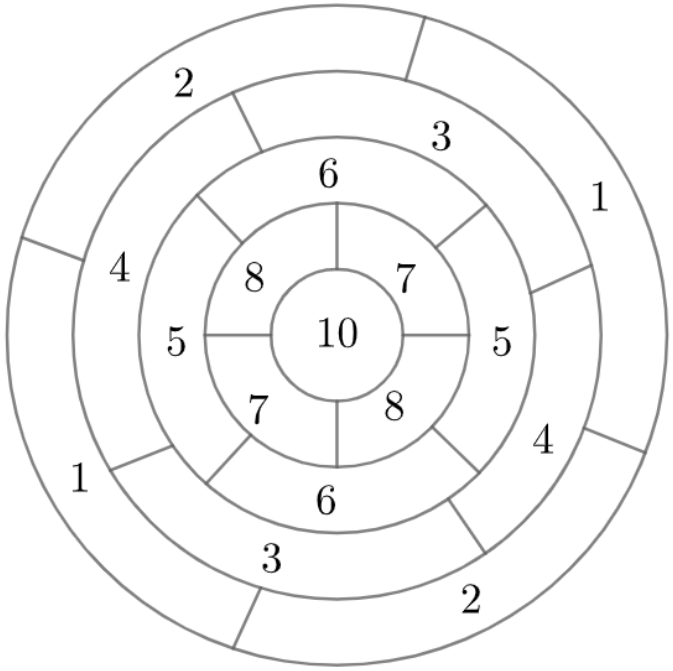
Какое максимальное количество баллов Света может набрать, если у неё есть пять дротиков и она будет очень стараться?
Задача 6.
Назовем натуральное число улиткой, если его запись состоит из записей трёх последовательных натуральных чисел, приписанных друг к другу в порядке возрастания: например, 111213 или 456. Сколько пятизначных чисел равны сумме двух улиток?
Задача 7.
Барон Мюнхгаузен утверждает, что существует такое натуральное число, что если его последнюю цифру переставить в начало, то получится новое число, которое в 4 раза больше исходного. Не ошибается ли барон?
Задача 8.
Числа от 1 до 20 разбили на две [непустые] группы и в каждой группе сосчитали среднее арифметическое. Может ли сумма этих двух средних быть равна 13?

