Задача 1.
Света записала на картонной полоске цифры сегодняшней даты – 05042021, – а потом разрезала полоску на 4 части так, что у неё получились 4 различных числа. Эти числа она сложила. Какая самая маленькая сумма могла у неё получиться? (Числа не могут начинаться с цифры 0, кроме числа нуль.)
Задача 2.
Шести из одиннадцати детей одной семьи задали вопрос: «Сколько у тебя сестёр?» Все шестеро ответили: «У меня 5 сестёр». Сколько в семье сыновей?
Задача 3.
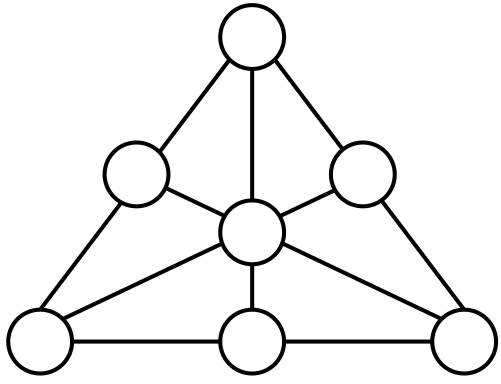
Можно ли вписать в кружочки на рисунке числа от 1 до 7 каждое по одному разу так, чтобы суммы трёх чисел на всех шести линиях на рисунке были одинаковыми?
Задача 4.
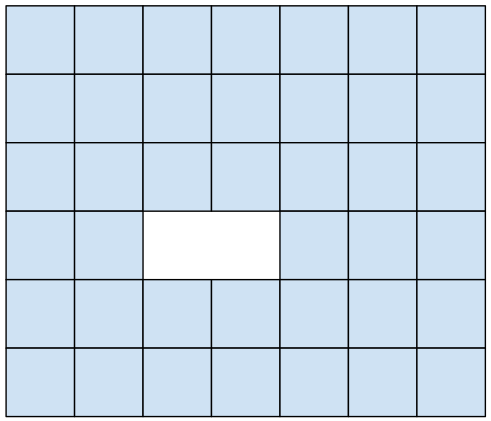
Из прямоугольника 6 × 7 вырезали доминошку 1 × 2 (см. рисунок). Разрежьте оставшуюся фигуру из 40 клеток на две одинаковые части по линиям сетки. Напоминаем, что фигуры называются одинаковыми, если их можно совместить наложением. Фигуры можно поворачивать и переворачивать.
Задача 5.
Произведение 4 различных натуральных чисел равно 144. Какое наименьшее значение может принимать их сумма?
Задача 6.
Назовём натуральное число 𝑛 триплетом, если оно равно сумме трёх различных натуральных чисел, причём второе из них делится на первое, а третье — на второе. Докажите, что каждое число, большее 24, — триплет.
Задача 7.
Из доски 100 × 100 по линиям сетки вырезано 1000 квадратов 2 × 2, не имеющих общих точек и не примыкающих к границе доски. Сколькими способами из оставшейся части доски можно вырезать ещё один квадрат 2 × 2?
Задача 8.
К левому берегу реки подошли 40 магов – 20 белых, один силы 2, каждый из остальных силы 1, и точно такая же по силам группа из 20 чёрных магов. Белые маги не согласны быть в лодке или на берегу вместе с чёрными, если там сумма сил чёрных больше, чем у белых. Когда лодка причаливает к берегу, все её пассажиры считаются находящимися на этом берегу. Как им всем с помощью трёхместной лодки переправиться на правый берег?

