Задача 1.
Докажите, что любое натуральное число вида 66...64 (число шестёрок не равно 0) можно представить в виде суммы двух нечётных составных чисел.
Задача 2.
Представим себе шахматную доску 3 × 4 (три столбца, четыре строки), в левом нижнем углу которой (на поле a1) стоит белый ферзь, а в правом верхнем (на поле c4) — чёрный король. Ферзь и король ходят по обычным правилам шахмат, первым ходит белый ферзь. Может ли ферзь добиться того, чтобы чёрный король оказался в правом нижнем углу доски (на поле c1)?
Задача 3.
Существует ли четырёхзначное число, не делящееся на 11, в котором нельзя заменить никакую одну цифру (возможно, даже на 0) так, чтобы получившееся в результате число делилось на 11?
Задача 4.
Каждая клеточка таблицы 99 × 99 покрашена в один из двух цветов – чёрный или белый. Известно, что каждая чёрная клетка не на границе таблицы имеет ровно 5 белых соседей (из 8), а каждая белая клетка не на границе таблицы имеет ровно 4 белых соседа (из 8). Сколько всего может быть чёрных клеток в этой таблице?
Задача 5.
Расставьте отсутствующие числа от 1 до 32 в строчку
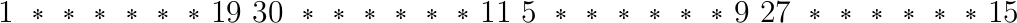
так, чтобы каждое из чисел использовалось в строчке ровно один раз, и чтобы сумма любых двух соседних чисел была квадратом натурального числа.
Задача 6.
За круглым столом в каком-то порядке сидят 12 человек, среди которых есть рыцари и лжецы. У каждого есть две карточки – красная и чёрная. Они по очереди передают своему соседу справа по одной карточке, причём рыцарь всегда передаёт карточку того же цвета, что и получил, а лжец – карточку другого цвета. Тот, кто передаёт карточку первым в круге, может выбрать для первого шага любую из своих карточек. Когда круг закончился, и у всех снова стало по две карточки, начинавший игру сказал «Мои карточки одинакового цвета». Сколько рыцарей могло быть за столом?

